Gvildenu | Mintys / 20160620Matematika

Matematikos išsiaiškinimo būdų apžvalga

Skaičiau šį pranešimą Lietuvos matematikų draugijos konferencijoje, 2016 m. birželio 20-21 d. O štai nuoroda į išsąmesnį straipsnį anglų kalba: Discovery in Mathematics: A System of Deep Structure.

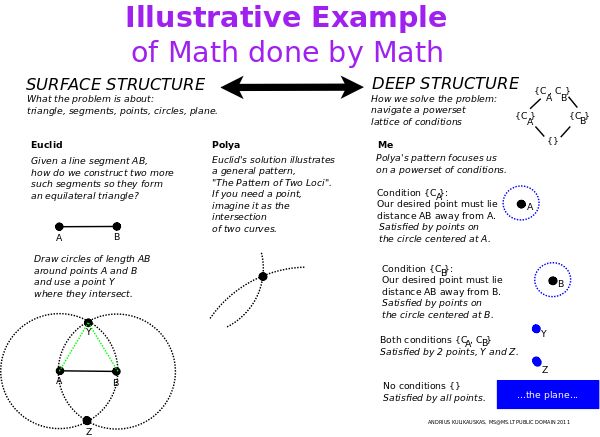
George Polyos knyga "Kaip išspręsti" (How to Solve It) iškėlė keturis pasikartojančius vaizduotės "derinius" kuriuos matematikai taiko spręsdami įvairių sričių uždavinius. Pavyzdžiui, esant segmentui AB, kaip jo pagrindu nubrėžti lygiakraštį trikampį? "Dviejų kreivių derinį" taikydami, apie taškus A ir B nubrėžiame apskritimus spinduliu AB ir įsidėmime jų sankirtų taškus. Pastebėkime, jog sprendžiant šį uždavinį, mūsų protas sustato sprendimo sąlygų gardelę: plokštuma (sąlygų nebuvimas), apskritimas A (viena sąlyga), apskritimas B (kita sąlyga), sankirtos taškai (abi sąlygos). Tad paviršutiniškas uždavinys (nubrėžti trikampį) išsprendžiamas vaizduotei pasitelkus paprastesnę, giliau glūdinčią sandarą (sąlygų gardelę). Tai primena kalbotyrininko Noam Chomsky sintaksės teoriją bei architekto Christopher Alexander derinių kalbą.

Tokių uždavinio sprendimo būdų prisirinkau iš įvairių šaltinių, o ypač Paul Zeitz išsamios knygos "The Art and Craft of Problem Solving". Kiekvienas būdas remiasi matematikams gerai pažįstama sandara kuri tačiau lieka neišrašyta o tik protu taikoma. Galime tokias sandaras laikyti prigimtinėmis. Surinkau 24 tokius derinius ir juos išdėliojau taip, kad būtų galima pamanyti, jog tai išbaigtas rinkinys.

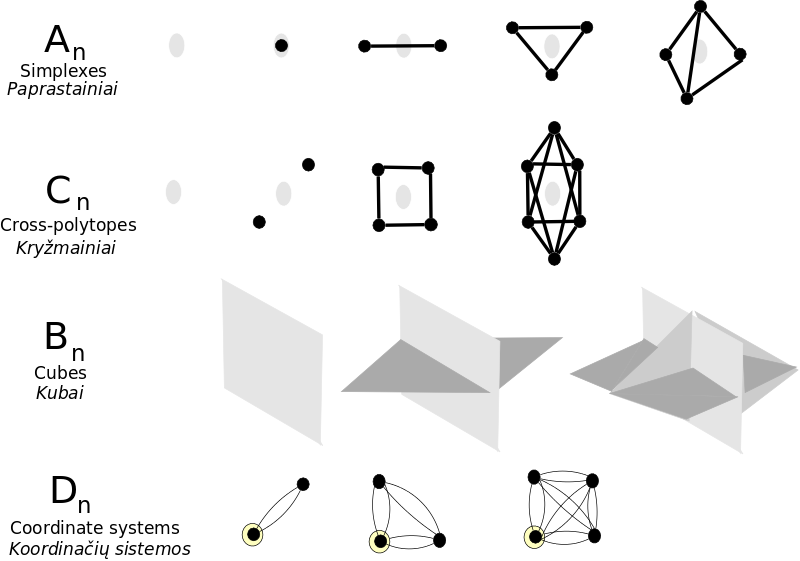
Pirmiausiai pamokysiu kaip dėsningai tverti keturias šeimas daugiamačių briaunainių, tai yra, politopų: An (simpleksus - paprastainius), Cn (ortopleksus - kryžmainius), Bn (kubus), Dn (demikubus - koordinačių sistemas). Jų simetrijų grupės yra taipogi klasikinių Lie algebrų šaknių sistemų Weyl'o grupės. Išryškės sandaros, veiksmai ir santykiai, kuriais dėsningai aptarsiu matematikos išsiaiškinimo būdus.

Įsivaizduokime briaunainio židinį. Paprastainiai kuriami prijungiant vis po vieną viršūnę kartu su briaunomis ją siejančias su jau esančiomis viršūnėmis. Židinys yra paprastainis be jokių viršūnių ir jos atrininkas, tai paprastainis Visuma susidaranti iš visų viršūnių. Kryžmainiai kuriami židiniui prijungiant vis po dvi viršūnes, nesusietomis viena su kita, tačiau susietomis su visomis kitomis viršūnėmis. Kryžmainiai turi Židnį bet neturi Visumos. Tuo tarpu kubai turi Visumą tačiau neturi Židinio. Juos Visuma sukuria atveriant seką stačiakampių veidrodžių. Demikubai neturi nė Židinio, nė Visumos. Tai koordinačių sistemos, kurios yra tarsi perpus įlenktas kubas, arba paprastainis su dvigubomis briaunomis ir išskirtinę viršūnę, koordinačių sistemos pradžią.

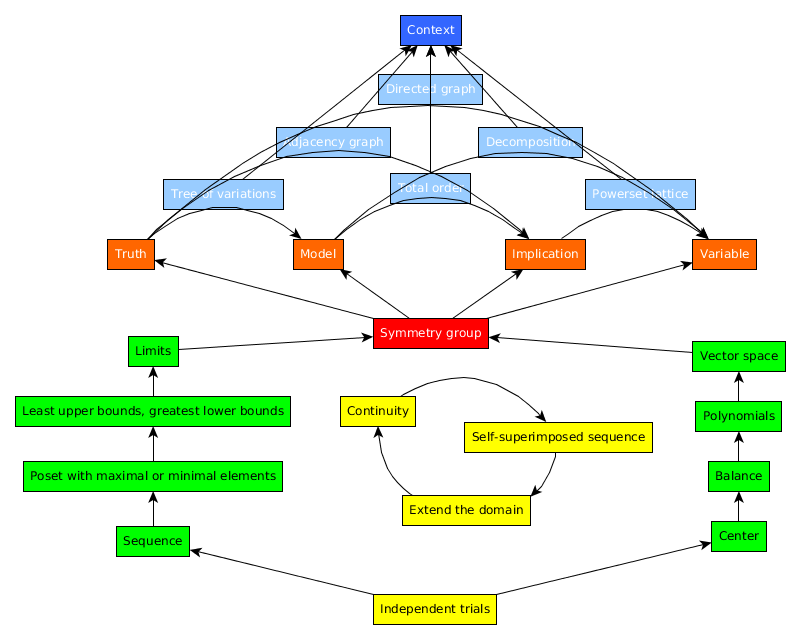
Keturių rūšių briaunainiai grindžia keturias geometrijas ir metalogikas. Paprastainiai iš Židinio siekia visą erdvę ir tad grindžia kryptis išsaugojančią paprastąją geometriją. Jais modeliuojama tiesa ir netiesa, pavyzdžiui, prieštaravimo būdu. Kryžmainiai apibrėžia priešingas kryptis ir užtat grindžia tieses išsaugojančią projekcinę geometriją. Jais kuriami metmenys, atrenkant svarbiausius matavimus. Kubai sieja stačiakampes kryptis ir užtat grindžia kampus išsaugojančią konformalią geometriją. Jais mąstome išvirkščiai, išsiaiškiname, kaip išvestas taškas kyla iš teiginių erdvių. Koordinačių sistemos derina kryptis ir kampus, todėl grindžia plotus išsaugojančią simplektinę geometriją. Jomis išsiaiškiname tiesų tikslingumą permąstydami kintamuosius, jais atskirdami šių keturių geometrijų semiotinius nesutapimus. Pavyzdžiui, brėždami brėžinį galime pagauti skirtumą tarp priklausomųjų ir nepriklausomųju kintamųju, žinomųjų ir nežinomųjų, duotųjų ir neapibrėžtųjų, nustatytųjų ir laisvųjų r t.t.

Mes galime kiekvieną geometriją suvokti, kaip siejančią lakšte išrašytą matematiką ir mūsų vaizduotės matematinę veiklą. Vienas išsiaiškinimo būdas yra tiesiog suvokti, jog visada galime atverti naują lakštą. Kitas būdas yra savo lakštą galutinai sutvarkyti, kad mūsų protas tarsi simetrijos grupė gali ją varstyti veiksmų sekomis, veiksmus dėlioti arba apgręžti. Trečias būdas yra suvokti, jog mūsų visą žinojimą sąlygoja aplinkybės. Jei jūsų paklausiu, kiek yra 10 ir 4? Jūs man galite pasakyti 14, bet atsakymas bus 2, nes turiu mintyje laikrodį.

Kaip bebūtų, siekiame sukurti simetrijos grupę, kuri suvestų algebraines sandaras ir analitinius vyksmus. Keturios briaunainių rūšys vaizduoja, kaip algebrainė sandara išryškina uždavinį. Paprastainis skatina suvokti uždavinio visumos židinį. Kryžmainiai skatina lyginti priešingybes, pavyzdžiui, kurie nariai priklauso poaibei ir kurie priklauso jos papildiniui. Kubai skatina lyginti kiekiais ir vienetais išreikštas sumas. Koordinačių sistemos skatina vektorinę erdvę tvarkingai tverti ar išardyti jos kanoninės bazių narių eilės tvarka.

Keturios briaunainių šeimomis taip pat savitai įžvelgiame analitinius vyksmus, kuriuos įsivaizduojame ne paskirame vaizduotės lakšte, o tų lakštų sekos pavyzdžiu. Galime remtis matematikos indukcija, simplekso židinio pavyzdžiu, kaip jisai sutveria vis naują viršūnę. Kryžmainių įkvėpti, galime įsivaizduoti bet kurio matavimo didžiausiają reikšmę ir mažiausiąją reikšmę. Kubų skilčių daugiamatiškumas leidžia mums suvokti tikslųjų viršutinių ir apatinių rėžių paiešką. Koordinačių sistemų dvilypiškumu įsivaizduojame, jog simplekso tveriama seka priartės ribą kažkur puskubyje.

Taip pat įsivaizduojame funktorius siejančius algebrainę sandarą ir analitinį vyksmą moksliniu metodu: nusistatymu, vykdymu ir permąstymu. Turint sudėties formulę, pavyzdžiui tą, kuria dvejetą keliame laipsniu iksas ir ygrikas, nusistatome pratęsdami jos galiojimo sritį, ją taikydami nuliui, neigiamiems skaičiams, trupmenoms ir t.t. Toliau, kintamuosius galime tolydžiai keisti, tokiu būdu tiriant ar modelis galios ar sublukš. Galiausiai, apibrendiname šią sąlygą ją lyginant su savimi, jos esmę išgryninant generuojančiąja funkcija.

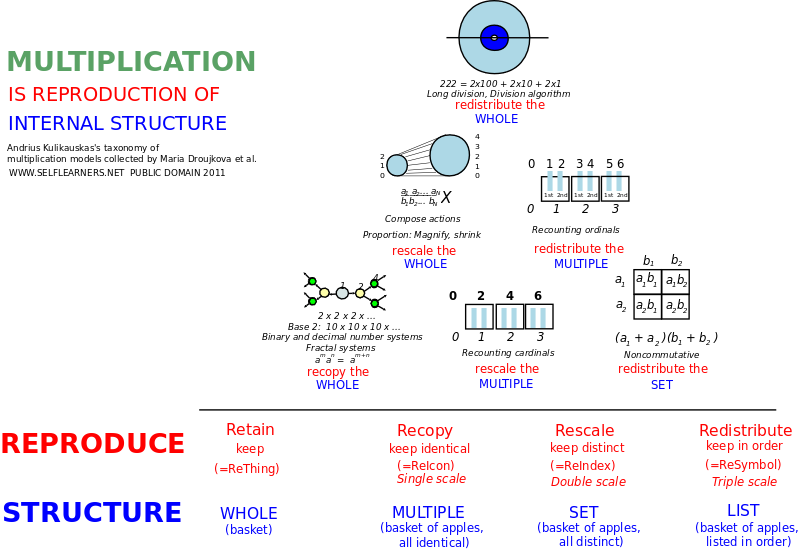
Kuomet turime simetrijos grupę ir apibrėžtą sistemą, tuomet savo keturiomis geometrijomis įsivaizduojame atitinkamas metalogikas, kuriomis sulyginame požiūrius matematinėje sistemoje ir už jos. Tačiau simetrija taip pat mums leidžia mąstyti laisvesnius ekvivalentumus, lygiavertiškumus šešiomis logikos transformacijomis, permainomis, kurios sistemos analitinį vyksmą taiko posistemės algebrainei sandarai. Galime visas įmanomas permainas pavaizduoti daugybos pavyzdžiais.

Protu įsivaizduojame fraktalinius savastinius panašumus daugindami visumą, kaip kad dvejetą keldami laipsniu.
Santykių daugyba siejame platesnius ir siauresnius žvilgsnius, permatuojame visumą.
Permatuojame kartotinius skaičiuodami po kelis.
Perskirstome aibę dėžučių daugyba, kuria išskiriame junginius ir bei ar, taikome sąlygų gardelę.
Perskirstome kartotinius skaidydami sandus, pertvarkydami vienetus.
Perskirstome visumą dalyba su liekana.

Apžvelgiant visus matematikos išsiaiškinimo būdus, esminis siekis yra nustatyti simetrijos grupę kuria galime tirti apibrėžtą sistemą. Simetrijos grupę ir atitinkamą sistemą suvedame moksliniu metodu susiedami algebraines sandaras ir analitinius vyksmus. Moksliniu metodu vis naujai praplėčiame dėsningumo galiojimo sritį, vis naujai tiriame tolydžiai ir vis naujai apibendriname generuojančia funkcija. Sistema nagrinėjama keturiomis geometrijomis ir atitinkamomis metalogikomis, kurios savaip tapatina požiūrį už sistemos su požiūriu sistemoje. Simetrijos grupė permainomis sieja skirtingų geometrijų apibrėžtus sistemos ir posistemės požiūrius. Šios permainos išsako laisvus ekvivalentumus, kuriais gali tekti visiškai naujai įvertinti visas aplinkybes ir pradėti visai nauju lakštu. Matematika dėsningai siekia tvarkos, visgi yra tobulai lanksti.