Mintys.LieSandarųIštakos istorija
Paslėpti nežymius pakeitimus - Rodyti kodo pakeitimus
Birželio 19 d., trečiadienį, 16:15-16:30, 416 aud., LKA ramovė, Šilo g. 5A, Lietuvos matematikų draugijos 60-oji konferencija, programa.
2019 m. birželio mėn. 19 d., trečiadienį, 16:15-16:30, 416 aud., LKA ramovė, Šilo g. 5A, Lietuvos matematikų draugijos 60-oji konferencija, programa.
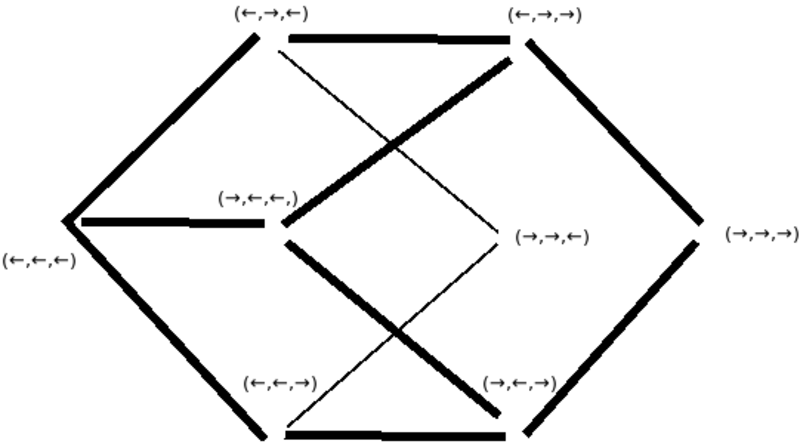
Simetriškas priešingybes vaizduoja koordinačių sistemos. Koordinates išsakysiu strėlėmis, į kairę ir į dešinę, kad jų simetriškumas būtų akivaizdus. Kubo aštuonios viršūnės išsidėsto pagal Paskalio trikampį. Kubą galime atitinkamai supjaustyti. Šitaip mąstant kubas nėra politopas, jis nesusideda iš politopų, nėra židinio, nė visumos. Šis kūbas susideda iš ašių, tad jo viršūnės yra savybių rinkiniai. Kiekvienu klausimu, kiekviename mate, kiekvienoje ašyje pasirinkta vienaip arba kitaip. Užtat sukeitus visas strėles į kairę ir į dešinę niekas iš esmės nepasikeistų, nes tai iš tiesų tėra semantinis skirtumas, priklausantis nuo visuminio konteksto, ką reiškia strėlė į kairę ir strėlė į dešinę. Užtat tokios koordinačių sistemos simetrijų grupę tenka padalinti iš dviejų. Simplekso simetrijas išsako simetrinė grupė, o koordinačių sistemos simetrijas išsako hyperoktahedrinės grupės pogrupė.
Simetriškas priešingybes vaizduoja koordinačių sistemos. Koordinates išsakysiu strėlėmis, į kairę ir į dešinę, kad jų simetriškumas būtų akivaizdus. Kubo aštuonios viršūnės išsidėsto pagal Paskalio trikampį. Kubą galime atitinkamai supjaustyti. Šitaip mąstant kubas nėra politopas, jis nesusideda iš politopų, nėra židinio, nė visumos. Šis kūbas susideda iš ašių, tad jo viršūnės yra savybių rinkiniai. Kiekvienu klausimu, kiekviename mate, kiekvienoje ašyje pasirinkta vienaip arba kitaip. Užtat sukeitus visas strėles į kairę ir į dešinę niekas iš esmės nepasikeistų, nes tai iš tiesų tėra semantinis skirtumas, priklausantis nuo visuminio konteksto, ką reiškia strėlė į kairę ir strėlė į dešinę. Užtat tokios koordinačių sistemos simetrijų grupę tenka padalinti iš dviejų. Simplekso simetrijas išsako simetrinė grupė, o koordinačių sistemos simetrijas išsako [hiperoktahedrinės grupės pogrupė].
Simetriškas priešingybes vaizduoja koordinačių sistemos. Koordinates išsakysiu strėlėmis, į kairę ir į dešinę, kad jų simetriškumas būtų akivaizdus. Kubo aštuonios viršūnės išsidėsto pagal Paskalio trikampį. Kubą galime atitinkamai supjaustyti. Šitaip mąstant kubas nėra politopas, jis nesusideda iš politopų, nėra židinio, nė visumos. Šis kūbas susideda iš ašių, tad jo viršūnės yra savybių rinkiniai. Kiekvienu klausimu, kiekviename mate, kiekvienoje ašyje pasirinkta vienaip arba kitaip. Užtat sukeitus visas strėles į kairę ir į dešinę niekas iš esmės nepasikeistų, nes tai iš tiesų tėra semantinis skirtumas, priklausantis nuo visuminio konteksto, ką reiškia strėlė į kairę ir strėlė į dešinę. Užtat tokios koordinačių sistemos simetrijų grupę tenka padalinti iš dviejų. Simplekso simetrijas išsako simetrinė grupė, o koordinačių sistemos simetrijas išsako alternatyvi grupė.
Simetriškas priešingybes vaizduoja koordinačių sistemos. Koordinates išsakysiu strėlėmis, į kairę ir į dešinę, kad jų simetriškumas būtų akivaizdus. Kubo aštuonios viršūnės išsidėsto pagal Paskalio trikampį. Kubą galime atitinkamai supjaustyti. Šitaip mąstant kubas nėra politopas, jis nesusideda iš politopų, nėra židinio, nė visumos. Šis kūbas susideda iš ašių, tad jo viršūnės yra savybių rinkiniai. Kiekvienu klausimu, kiekviename mate, kiekvienoje ašyje pasirinkta vienaip arba kitaip. Užtat sukeitus visas strėles į kairę ir į dešinę niekas iš esmės nepasikeistų, nes tai iš tiesų tėra semantinis skirtumas, priklausantis nuo visuminio konteksto, ką reiškia strėlė į kairę ir strėlė į dešinę. Užtat tokios koordinačių sistemos simetrijų grupę tenka padalinti iš dviejų. Simplekso simetrijas išsako simetrinė grupė, o koordinačių sistemos simetrijas išsako hyperoktahedrinės grupės pogrupė.
Ačiū Rimvydui Krasauskui už pabendravimus šiais klausimais.
Keturių klasikinių Lie grupių ir algebrų kombinatorinės ištakos
Keturių klasikinių Lie grupių ir algebrų kombinatorinės ištakos
Žr. Classical Lie Algebras, Santrauka, Juodraštis
Birželio 19 d., trečiadienį, 16:15-16:30, 416 aud., LKA ramovė, Šilo g. 5A, Lietuvos matematikų draugijos 60-oji konferencija, programa, informacija registravimui
Birželio 19 d., trečiadienį, 16:15-16:30, 416 aud., LKA ramovė, Šilo g. 5A, Lietuvos matematikų draugijos 60-oji konferencija, programa.
[10 Apžvalga]
Visa tai apžvelgiant, sakyčiau, kad A šeima išreiškia simpleksų simetriją ir kompleksiniais skaičiais griežtai skiria skaičiavimą pirmyn ir atgal, tarp židinio kuriame nieko nėra ir visumos, kuriame yra viskas. D šeima išreiškia koordinačių sistemų simetriją, tarsi reliatyvų kubą, ir savo reliatyvumu neskiria skaičiavimo pirmyn bei atgal. B šeima išreiškia hiperkubus, skaidančius absoliučią visumą, kuris yra tasai jų papildomas nulis, tačiau galima sakyti, nuo tos visumos skaičiuoja tiktai atgal, užtat išsikvepia. Šios dvi šeimos panaikina skaičiavimo krypčių skirtumą, iš kompleksinių skaičių padaro realiuosius skaičiau. Tuo tarpu D šeima išreiškia kryžminius politopus, kaip kad ortohedrą, kuriais galima skaičuoti pirmyn iš židinio ir pasiekti ją supančią plokštumų, langelių dangą, skiriančią vidų ir išorę, taip kad galima praplėsti skaičiavimą, jį pasukant pirmyn ir atgal, ir tokiu būdu kvaternionais praplėsti kompleksinius skaičius. Toliau bandyčiau susieti šias keturias simetrijas, šias klasikines šeimas, su keturiomis geometrijomis: projektyvine, afinine, konformalia ir simplektine.
Visa tai apžvelgiant, sakyčiau, kad A šeima išreiškia simpleksų simetriją ir kompleksiniais skaičiais griežtai skiria skaičiavimą pirmyn ir atgal, tarp židinio kuriame nieko nėra ir visumos, kuriame yra viskas. D šeima išreiškia koordinačių sistemų simetriją, tarsi reliatyvų kubą, ir savo reliatyvumu neskiria skaičiavimo pirmyn bei atgal. B šeima išreiškia hiperkubus, skaidančius absoliučią visumą, kuris yra tasai jų papildomas nulis, tačiau galima sakyti, nuo tos visumos skaičiuoja tiktai atgal, užtat išsikvepia. Šios dvi šeimos panaikina skaičiavimo krypčių skirtumą, iš kompleksinių skaičių padaro realiuosius skaičiau. Tuo tarpu D šeima išreiškia kryžminius politopus, kaip kad ortohedrą, kuriais galima skaičuoti pirmyn iš židinio ir pasiekti ją supančią plokštumų, langelių dangą, skiriančią vidų ir išorę, taip kad galima praplėsti skaičiavimą, jį pasukant pirmyn ir atgal, ir tokiu būdu kvaternionais praplėsti kompleksinius skaičius. Toliau bandyčiau susieti šias keturias simetrijas, šias klasikines šeimas, su keturiomis geometrijomis: projektyvine, afinine, konformalia ir simplektine.
Žr. Santrauka, Juodraštis
[00 Įvadinis]
[01 Simetrijos pavyzdžiai]

[02 Simpleksų generavimas]
[03 Koordinačių sistemos]
[04 Kryžminiai politopai]
[05 hiperkubai]
[06 Keturios galimybės]

[07 Skaičiavimai]
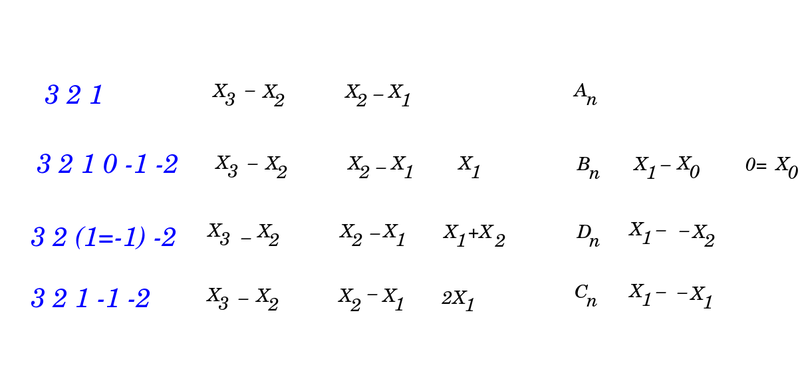
[08 Angų sistemos]
[09 Atvirkštinės]
Birželio 19 d., trečiadienį, 16:15-16:30, 416 aud., LKA ramovė, Šilo g. 5A, Lietuvos matematikų draugijos 60-oji konferencija, programa, informacija registravimui
- simpleksais: išsirinkti ar neišsirinkti
- kryžminiais politopais: išsirinkti vienaip ar išsirinkti kitaip ar neišsirinkti
- hiperkubais: išsirinkti ar neišsirinkti vienaip ar neišsirinkti kitaip
- koordinačių sistemomis: išsirinkti vienaip ar išsirinkti kitaip - arba tolygiai - neišsirinkti vienaip ar neišsirinkti kitaip
- simpleksais: parinkti ar neparinkti
- kryžminiais politopais: pasirinkti vienaip ar pasirinkti kitaip ar neparinkti
- hiperkubais: parinkti ar nepasirinkti vienaip ar nepasirinkti kitaip
- koordinačių sistemomis: pasirinkti vienaip ar kitaip - arba tolygiai - nepasirinkti vienaip ar nepasirinkti kitaip
[02 Simetrijos pavyzdžiai]
[01 Simetrijos pavyzdžiai]
[03 Simpleksų generavimas]
[02 Simpleksų generavimas]
[04 Koordinačių sistemos]
[03 Koordinačių sistemos]
[05 Kryžminiai politopai ir hiperkubai]
[04 Kryžminiai politopai]
[05 hiperkubai]
Kaip intuityviai suprasti? Išdėstysiu sąvokas, kurios manau yra svarbios.
I) Matematikos žemėlapis ir Lie algebros, Lie grupės
- Tariamai ar tikrai gyvenimiškai: klasifikavimo išdavos - Dynkin diagramos
II) Sandaugos simetrijos
- politopai - priešingybės
III) Nulis
- Šaknų sistemos - apsisukimai
IV) Atvirkštinės matricos
- Skaičiai - realusis: posūkis taške - joks, kompleksinis: posūkis apskritime, kvaternionas: posūkis sferoje
- Ortogonališkumas (eilučių ir stulpelių) Orthogonality of rows and columns - transpose is inverse.
- Cayley-Dickson konstrukcija
- Kaip susikabina posūkiai
- Komutatyvumas - apskritimas - nulis
- Posūkių grupės - aspkritimas, sfera
V) Keturios geometrijos
Visa tai apžvelgiant, sakyčiau, kad A šeima išreiškia simpleksų simetriją ir kompleksiniais skaičiais griežtai skiria skaičiavimą pirmyn ir atgal, tarp židinio kuriame nieko nėra ir visumos, kuriame yra viskas. D šeima išreiškia koordinačių sistemų simetriją, tarsi reliatyvų kubą, ir savo reliatyvumu neskiria skaičiavimo pirmyn bei atgal. B šeima išreiškia hiperkubus, skaidančius absoliučią visumą, kuris yra tasai jų papildomas nulis, tačiau galima sakyti, nuo tos visumos skaičiuoja tiktai atgal, užtat išsikvepia. Šios dvi šeimos panaikina skaičiavimo krypčių skirtumą, iš kompleksinių skaičių padaro realiuosius skaičiau. Tuo tarpu D šeima išreiškia kryžminius politopus, kaip kad ortohedrą, kuriais galima skaičuoti pirmyn iš židinio ir pasiekti ją supančią plokštumų, langelių dangą, skiriančią vidų ir išorę, taip kad galima praplėsti skaičiavimą, jį pasukant pirmyn ir atgal, ir tokiu būdu kvaternionais praplėsti kompleksinius skaičius. Toliau bandyčiau susieti šias keturias simetrijas, šias klasikines šeimas, su keturiomis geometrijomis: projektyvine, afinine, konformalia ir simplektine.
Tai jau žingsnis pirmyn link paaiškinimo kurio ieškau. Manau, jis taip pat gali padėti suprasti realiųjų skaičių, kompleksinių skaičių ir kvaternionų vaidmenį. Mat A šeima susijusi su unitarinėmis matricomis, su kompleksinių skaičių norma, su posūkiais kompleksinių skaičių daugiamatėje erdvėje, tad skaičiavimo dualizmas gali glūdėti kompleksinių skaičių jungtiniuose. B ir D šeimos susijusios su neporinių ir porinių dimensijų ortogonalinėmis matricomis, su realųjų skaičių norma, su posūkiais realųjų skaičių daugiamatėje erdvėje. Jas galima suprasti kaip skaičiavimo sukarpymą ir galus sudūrimą. Tuos galus galima sudurti papildomu matu, ir tokiu atveju bus neporinis matų skaičius. Arba galima du matus sutapatinti, kuriuo atveju yra porinis matų skaičius. O C šeima susijusi su simplektinėmis matricomis, su kvaternionų norma, su posūkiais kvartenionų daugiamatėje erdvėje. Ją galima suprasti kaip skaičiavimo sulankstymą, taip kad iš dviejų matų gaunasi keturi matai.
Prisipažįstu, aš kol kas tik pradinukas bandydamas įsivaizduoti posūkius ir kaip juos vaizduoti matricomis, kurių nariai gali būti realieji skaičiai, kompleksiniai skaičiai arba netgi kvaternionai. Paprasčiausi yra posūkiai apskritime, kuriuos galima vaizduoti realiųjų skaičių matricomis dviem eilutėm ir dviem stulpeliais, arba vienu kompleksiniu skaičiumi. Šie posūkiai yra komutatyvūs, užtat neįdomūs, tarsi nuliniai. Tačiau šį apskritimą, kurio posūkiai sukasi apie {$z$} ašį, galime papildyti posūkiais apie {$x$} ir {$y$} ašis. Šiuos posūkius apie sferą galima pavaizduoti vienu kvaternionu. Dabar jau atsiranda nekomutatyvumas. Posūkis apie {$x$} ir paskui {$y$} skiriasi nuo posūkio apie {$y$} ir paskui {$x$}. Atsiranda tarsi sankaba tarp šių dviejų galimybių ir jų ryšį išreiškia komutatorius XY-YX = [X,Y]. Kai šis komutatorius nulinis, tai posūkiai nesusiję, bet kai jis nenulinis, tai posūkiai sąveikauja, o būtent tai mus domina. Turbūt ne tik man yra sunku įsivaizduoti posūkius keturmatėse ir penkiamatėse erdvėse, nes Lie grupių klausimai nagrinėjami Lie algebromis, kurie susieti eksponencialu, taip kad posūkių daugybos klausimai virsta sankabų sudėties klausimais.
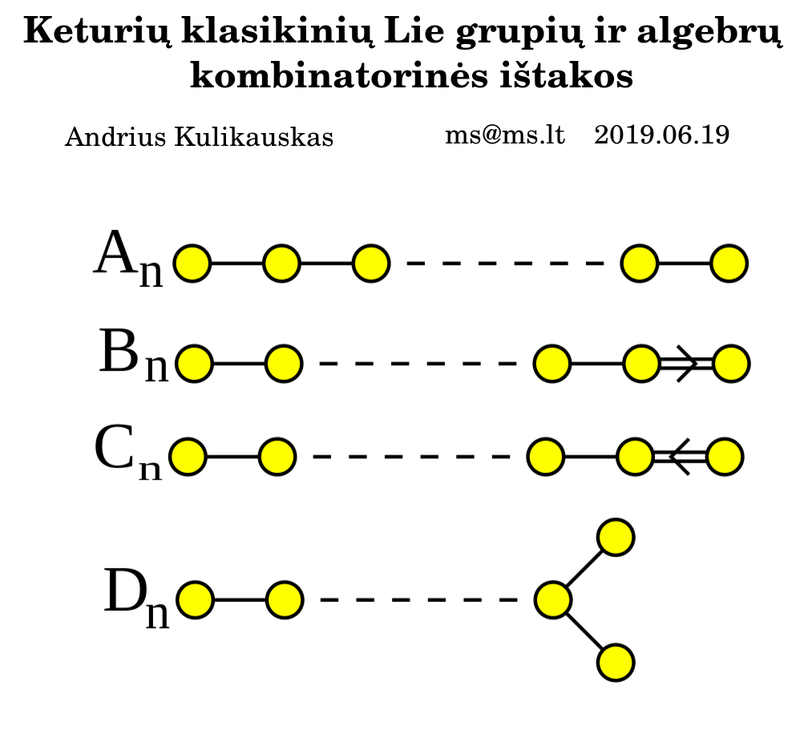
Dynkin diagrama vaizduoja Lie algebros paprastasias šaknis, tai yra, vienamates erdves, kurių prireikia nusakant Lie grupės posūkius. Kiekvienas rutulėlis yra vienamatė erdvė, šaknis, vektorius, tarsi ta sankaba siejanti sferos posūkius. Dynkin diagrama koduoja ryšius tarp šaknų, tarp tų sankabų. Geometriškai, dvigubas ryšys tarp šaknų reiškia jas skiria 135 laipsnių kampas, viengubas ryšys tarp šaknų reiškia jas skiria 120 laipsnių kampas, o jeigu nėra ryšio tarp šaknų, tai jas skiria 90 laipsnių kampas, vadinasi, jos yra ortogonalios, nesąveikauja. Žodžiu, šaknų sąveikavimas labai ribotas, jos vienas kitai beveik visada ortogonalios. Įsidėmėkime, kad visos keturios klasikinės šeimos yra labai panašios, skiriasi tiktai galūnės. Kiekvienu atveju stuburą daro šaknų grandinė. 120 laipsnių kampu pereiname iš pirmos šaknies į antrą šaknį, ir 120 laipsnių kampu pereiname iš antros šaknies į trečią šaknį, tačiau pirmą ir trečią šaknį skiria būtent 90 laipsnių, taip kad jos tiesiogiai nesąveikauja. Ir taip per visą grandinę ir kitokių grandinių negali būti. Tad labai įdomu, kas darosi tose galūnėse.
Aišku, nelengva įsivaizduoti šias daugiamates sistemas, tačiau kai kurios galūnės yra dvimatės sistemos. Šie keli pavyzdžiai pavaizduoja šaknų sistemų simetriškumą. Kiekviena šaknis α nusako savitą kryptį, ir kaip normali vektorė apibrėžia hiperplokštumą. Visų šaknų atspindžiai kitapus tos hiperplokštumos taipogi bus šaknys, įskaitant ir −α. Užtat jeigu dvi šaknis skiria daugiau kaip 90 laipsnių kampas, tai jų sudėtis bus šaknis. Ir jeigu dvi šaknis skiria mažiau kaip 90 laipsnių kampas, tai jų skirtumas bus šaknis. Bet jeigu šaknis skiria lygiai 90 laipsnių kampas, tai jų sudėtis ar skirtumas gali būti ar nebūti šaknų sistemoje, žiūrint kokia sistema. Šiaip kai šaknis skiria 120 laipsnių kampas, kaip kad šaknų grandinėje, tai visos šaknys yra tokio pat ilgio. Tačiau galūnėje paskutinę šaknį gali skirti 135 laipsnių kampas, kuomet jinai bus už visas kitas trumpesnė arba už visas kitas ilgesnė.
Šaknų sistemos yra navigacinės sistemos. Svarbu, kad neatsirastų dvi šaknys rodančios ta pačia kryptimi. Tokiu atveju visa sistema subliukštų, tai yra, atitinkama Cartano matrica išsigimtų, neturėtų atvirkštinės, jos determinantas būtų nulis. Galima įsitikinti, kad šaknų sistema negali susidaryti iš kubo šonų ir kampų, mat, tuomet kubo šono kryptimi atsirastų dvigubai ilgesnė šaknis. O tai reiškia, kad sistema negali neribotai augti trimis kryptimis ir iš esmės tegali augti, kaip grandinė.
Atvirkštinės matricos koduoja santykius tarp indeksus.
- Įvadas į Lie grupes ir algebras. Dykin diagrams. Rotations in 2, 3 dimensions. Lie algebra product [,] effect on basis elements of matrices - yeilding ei-ej, aij - arrow
- Tariamai ar tikrai gyvneimiškai
- Kaip [,] varžo Lie grupes? If XY=YX, then e^x e^y = e^{x+y} and [X,Y] =0 then dimensions are independent. e^X e^-X = e^I e^(ax+bx) = e^ax e^bx
- 4 geometrijos
- Conservation - paths, lines, angles, oriented areas. Sypmlectic 2x2 matrix: oriented area.
- inverses of group elements
- posūkiai turi determinantą 1. So by Cramer's rule they have combinatorially nice inverses.
- Inverse types
- Symplectic inverse. How does the symplectic inverse relate to the quaternions? to their conjugation?
- Why can't have other inverse types? For example, i to j iff j-bar to i-bar without sign change?
- Reorganize symplectic matrix in terms of 2x2 matrices. Get combinatorial interpretation of inverse elements.
- posūkiai - R, C, H - ir jų pavyzdžiai mažamatėse erdvėse
- e^tM reikšmės
- poliarinė dekompozicija
- bilinear forms
- matrix symmetries
- Cartan subalgebras
- generalized Cartan matrices
- Cartan matrix. Entries give the amount of looseness from root -i, how many steps can be taken with root j.
- Row of Cartan matrix. Given root -i, the various degrees of looseness one can take in the direction of each root.
- Determinant of Cartan matrix. Volume of looseness. Shows nondegeneracy of looseness in direction of each root. Volume spanned by row vectors giving looseness from each negative root. Volume spanned by column vectors giving amount of looseness in each direction. Size of WeightLattice/RootLattice which is the looseness of the whole system, the number of times the root system can be repeated in any dimension.
- Cartan matrix determinant. Study why An=n+1. A_n+1=2A_n-A_n-1Why the constraints arise for the other Lie algebra root system. Why the volume collapses for B_n, C_n, D_n. Why it's not possible to alter both ends.
- Determinant of Cartan matrix of G2 is 1. Explain why this is true. Based on Cartan matrix entries, based on weight lattice / root lattice.
- Root systems are variants of A_n simplex. Reverse the count? Why do the quadruple links arise. How does this relate to the Cartan matrix? And the weight lattice? and looseness? For B_n, are these double or quadruple links between x_i and 0?
- Weight/Root = 4 for A_3, show this with a 3-dimensional lattice
- Weight/Root lattice
- Counting <->
- Root systems - simplex enhancements
- Weyl groups
- Choice frameworks
- 120 + 120 = 90 degrees (ir Bott periodicity)
- Link An Lie algebra and Lie group
- An Geometric Link back bone for root systems
- A_2 illustration in 3 dimensions
- požiūriai, matai
Special linear groups of Reals, Complexes, Quaternions have maximal compact subgroups SO(n), SU(n), Sp(n).
Keturios klasikinės šeimos Lie grupių ir algebrų yra kertinės matematinės sandaros, siejančios algebrą ir analizę. Jų klasifikacija išplaukia iš Dynkin diagramų. Tai yra unitarinės {$A_n$}, neporinės ortogonalinės {$B_n$}, simplektinės {$C_n$} ir porinės ortogonalinės {$D_n$} grupės ir algebros. Ar galima giliau ir aiškiau įžvelgti, kokios yra šių keturių šeimų esminės savybės dėl kurių jos išsiskiria? Pristatysiu tris priėjimus ir savo pastangas juos susieti.
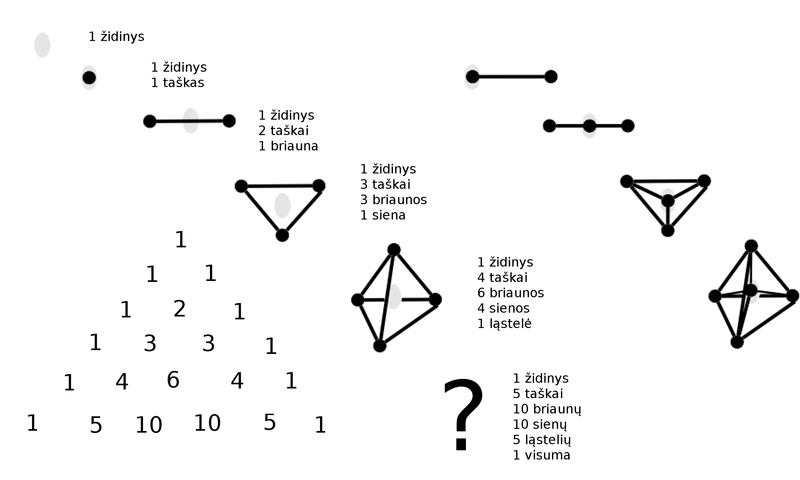
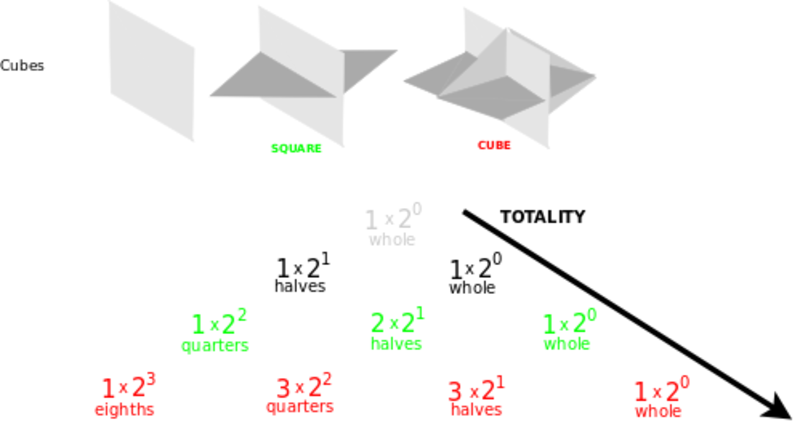
Pirma, Lie algebrų šaknų sistemas sietinos su jų simetrijas išreiškiančiomis Weyl grupėmis. Atitinkamas simetrijas turi trys politopų šeimos (simpleksai, kryžminiai politopai, hiperkubai) ir ketvirta sandara - hiperkubo koordinačių sistema. Šios keturios sandaros vaizduoja keturių skirtingų pobūdžio pasirinkimų kombinatorikas. Tai skirtingi būdai, kuriais protas įžvelgia simetriją Paskalio trikampiu generuojamoje sandaugoje {$x_1 x_2 \dots x_n$}. Pavyzdžiui, trikampis (simpleksas) turi vieną židinį, tris viršūnes, tris kraštus ir vieną visumą. O pastačius kūbą ant vienos viršūnės, jo aštuonios viršūnės išsidėsto: 1, 3, 3, 1. Atkreipiame dėmesį, kad šios simetrijos paviršutiniškai sutampa tačiau skiriasi savo sintaksine logika.
Antra, klasikinių Lie algebrų šaknų sistemos skirtingai auga. Visos grupės turi šaknis {$-x_1+x_2, -x_2 + x_3, \dots , -x_{n-1}+x_{n}$}. Grupės {$A_n$} šaknys auga toliau {$-x_n+x_{n+1}$}. Tačiau kitų grupių šaknys įvairiai sieja šį skaičiavimą pirmyn su skaičiavimu atgal {$-x_n-x_{n-1}, -x_{n-1}-x_{n-2}, \dots , -x_2-x_1$}. Grupė {$C_n$} juos suduria tiesiogiai, tarsi sulenkiant siūlą. Taip atsiranda šaknis {$-x_n -x_n = -2x_n$}. Grupė {$B_n$} tarsi karpo skaičiavimo siūlą ir sujungia abi dalis papildomu nuliu {$0$}. Taip atsiranda šaknis {$-x_n +0 = -x_n$}. Grupė {$D_n$} tarsi karpo skaičiavimo siūlą ir sutapatina abiejų dalių galus, taip kad {$-x_n = -x_n$} ir seka šaknis {$-x_n -x_{n-1}$}. Taigi, klasikinių Lie algebrų šaknų sistemos išsako santykį tarp skaičiavimo pirmyn ir skaičiavimo atgal.
Trečia, klasikines Lie grupes sudaro skirtingų dalybos algebrų isometrijos. Ortogonalinės, unitarinės, simplektinės grupės atitinkamai sudaro realųjų skaičių, kompleksinių skaičių, kvaternionų isometrijos.
Papasakosime, kaip sekasi tirti ir sieti šiuos tris skirtingus priėjimus, ir kaip jie atkreipia dėmesį į simetrijas glūdinčias pačioje matematikoje, paprasčiausiose jos ženklų išraiškose.
Visa tai apžvelgiant, sakyčiau, kad A šeima išreiškia simpleksų simetriją ir kompleksiniais skaičiais griežtai skiria skaičiavimą pirmyn ir atgal, tarp židinio kuriame nieko nėra ir visumos, kuriame yra viskas. D šeima išreiškia koordinačių sistemų simetriją, tarsi reliatyvų kubą, ir savo reliatyvumu neskiria skaičiavimo pirmyn bei atgal. B šeima išreiškia hiperkubus, skaidančius absoliučią visumą, kuris yra tasai jų papildomas nulis, tačiau galima sakyti, nuo tos visumos skaičiuoja tiktai atgal, užtat išsikvepia. Šios dvi šeimos panaikina skaičiavimo krypčių skirtumą, iš kompleksinių skaičių padaro realiuosius skaičiau. Tuo tarpu D šeima išreiškia kryžminius politopus, kaip kad ortohedrą, kuriais galima skaičuoti pirmyn iš židinio ir pasiekti ją supančią plokštumų, langelių dangą, skiriančią vidų ir išorę, taip kad galima praplėsti skaičiavimą, jį pasukant pirmyn ir atgal, ir tokiu būdu kvaternionais praplėsti kompleksinius skaičius. Toliau bandyčiau susieti šias keturias simetrijas, šias klasikines šeimas, su keturiomis geometrijomis: projektyvine, afinine, konformalia ir simplektine.
[Įvadinis]
[00 Įvadinis]
[Simetrijos pavyzdžiai]
[02 Simetrijos pavyzdžiai]
[Simpleksų generavimas]
[03 Simpleksų generavimas]
[Koordinačių sistemos]
[04 Koordinačių sistemos]
[Kryžminiai politopai ir hiperkubai]
[05 Kryžminiai politopai ir hiperkubai]
[Keturios galimybės]
[06 Keturios galimybės]
[Skaičiavimai]
[07 Skaičiavimai]
[Angų sistemos]
[08 Angų sistemos]
[Atvirkštinės]
[09 Atvirkštinės]
[Apžvalga]
[10 Apžvalga]
[Įvadinis]
[Simetrijos pavyzdžiai]
[Simpleksų generavimas]
[Koordinačių sistemos]
[Kryžminiai politopai ir hiperkubai]
[Keturios galimybės]
[Skaičiavimai]
[Angų sistemos]
[Atvirkštinės]
[Apžvalga]
Visa tai apžvelgiant, pastebėkime, kad trikampį galima geometriškai suprasti ir kaip tris takus vedantį ratu, ir kaip tris susikryžiuojančias tieses, ir kaip tris kampus, ir kaip iššluojamą orientuotą plotą. A šeima pagrįsta simpleksais, gimdančius vis naujus takus, griežtai skiriančius židinį kuriame nieko nėra ir visumą, kuriame viskas yra, tad kompleksiniais skaičiais griežtai skiriančius skaičiavimą pirmyn ir skaičiavimą atgal. Jinai gal grindžia projektyvinę geometriją. D šeima išsako kubus, tiktai ne absoliučiai, o reliatyviai, be jokios visumos, ir jinai gal grindžia tiesių geometriją, afininę geometriją. B šeima pagrįsta hiperkubais, pripažįstančius erdvės visumą, ją skaidančius erdvę į kampus, tad įsivaizduoju, grindžia konformalią geometriją. C šeima pagrįsta kryžminiais politopais, kaip kad oktahedru, pripažįstančius židinį, gimdančius viršūnių poras, tad ašis, ir jais grindžiančius plokštumas, tad skiriančius vidų ir išorę. Šios plokštumos, įsivaizduoju, susijusios su kvaternionais, ir grindžia simplektinę geometriją.
Visa tai apžvelgiant, sakyčiau, kad A šeima išreiškia simpleksų simetriją ir kompleksiniais skaičiais griežtai skiria skaičiavimą pirmyn ir atgal, tarp židinio kuriame nieko nėra ir visumos, kuriame yra viskas. D šeima išreiškia koordinačių sistemų simetriją, tarsi reliatyvų kubą, ir savo reliatyvumu neskiria skaičiavimo pirmyn bei atgal. B šeima išreiškia hiperkubus, skaidančius absoliučią visumą, kuris yra tasai jų papildomas nulis, tačiau galima sakyti, nuo tos visumos skaičiuoja tiktai atgal, užtat išsikvepia. Šios dvi šeimos panaikina skaičiavimo krypčių skirtumą, iš kompleksinių skaičių padaro realiuosius skaičiau. Tuo tarpu D šeima išreiškia kryžminius politopus, kaip kad ortohedrą, kuriais galima skaičuoti pirmyn iš židinio ir pasiekti ją supančią plokštumų, langelių dangą, skiriančią vidų ir išorę, taip kad galima praplėsti skaičiavimą, jį pasukant pirmyn ir atgal, ir tokiu būdu kvaternionais praplėsti kompleksinius skaičius. Toliau bandyčiau susieti šias keturias simetrijas, šias klasikines šeimas, su keturiomis geometrijomis: projektyvine, afinine, konformalia ir simplektine.
Visa tai apžvelgiant, pastebėkime, kad trikampį galima geometriškai suprasti ir kaip tris takus vedantį ratu, ir kaip tris susikryžiuojančias tieses, ir kaip tris kampus, ir kaip iššluojamą orientuotą plotą. A šeima pagrįsta simpleksais, gimdančius vis naujus takus, griežtai skiriančius židinį kuriame nieko nėra ir visumą, kuriame viskas yra, tad kompleksiniais skaičiais griežtai skiriančius skaičiavimą pirmyn ir skaičiavimą atgal. B šeima pagrįsta kryžminiais politopais, pripažįstančius nulį, gimdančius viršūnių poras, tad ašis, tieses. D šeima pagrįsta hiperkubais, pripažįstančius erdvės visumą, ją skaidančius erdvę į kampus
Visa tai apžvelgiant, pastebėkime, kad trikampį galima geometriškai suprasti ir kaip tris takus vedantį ratu, ir kaip tris susikryžiuojančias tieses, ir kaip tris kampus, ir kaip iššluojamą orientuotą plotą. A šeima pagrįsta simpleksais, gimdančius vis naujus takus, griežtai skiriančius židinį kuriame nieko nėra ir visumą, kuriame viskas yra, tad kompleksiniais skaičiais griežtai skiriančius skaičiavimą pirmyn ir skaičiavimą atgal. Jinai gal grindžia projektyvinę geometriją. D šeima išsako kubus, tiktai ne absoliučiai, o reliatyviai, be jokios visumos, ir jinai gal grindžia tiesių geometriją, afininę geometriją. B šeima pagrįsta hiperkubais, pripažįstančius erdvės visumą, ją skaidančius erdvę į kampus, tad įsivaizduoju, grindžia konformalią geometriją. C šeima pagrįsta kryžminiais politopais, kaip kad oktahedru, pripažįstančius židinį, gimdančius viršūnių poras, tad ašis, ir jais grindžiančius plokštumas, tad skiriančius vidų ir išorę. Šios plokštumos, įsivaizduoju, susijusios su kvaternionais, ir grindžia simplektinę geometriją.
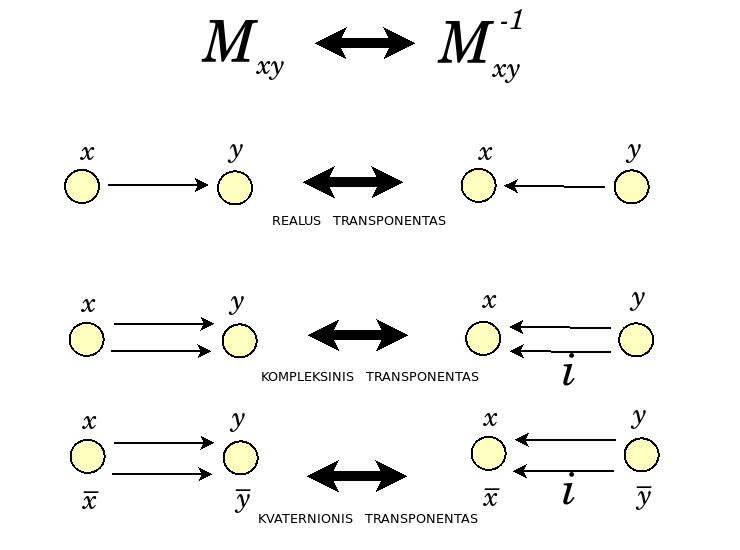
Posūkių matricos determinantas yra vienas. Tai reiškia, kad Kreimerio taisykle apskaičiuojant atvirkštinę, nereikia rūpintis vardikliu, yra tik skaitiklis, kas kombinatorikai itin dėkinga. Iš tiesų, posūkių matricų stulpeliai ir eilutės yra, kaip vektoriai, tampriai susiję. Realiųjų skaičių atveju stulpeliai ir eilutės yra ortonormiški. Užtat ortogonalinės matricos atvirkštinė prilygsta transponuotai matricai. Unitariosios matricos atvirkštinė yra kompleksiškai jungtinė ir transponuota matrica. Supraskime matricos narį kaip taką iš indekso i į indeksą j. Ortogonalinės matricos atveju, atitinkamas atvirkštinės narys išsakys taką atgal iš indekso j į indeksą i. Unitariosios matricos atveju teks papildomai parinkti kompleksišką jungtinę, kas išlaiko skirtumą tarp dviejų krypčių. Simplektinės matricos atveju matricas pasidalina į 2x2 kvadratėlius. Kvadratėlis nusako keturis takus tarp dviejų indeksų turinčių po dvi angas. Du takai veda iš kairės į dešinę ir iš dešinės į kairę. Tiesiog pakeičiame jų kryptį. Likę du takai veda iš kairės į kairę ir iš dešinės į dešinę. Mes taipogi pakeičiame jų kryptį, tačiau taip pat padauginame iš -1, kaip dera skiriant kompleksines jungtines. Tokiu būdu šie keturi takai pasidalina kaip kad kvarternionas pasidalina į du kompleksinius skaičius, nusakančius poziciją ir judesio kiekį, taip kad atvirkštinė išsako kvaternioniškai jungtinė ir transponuota matricą.
Posūkių matricos determinantas yra vienas. Tai reiškia, kad Kreimerio taisykle apskaičiuojant atvirkštinę, nereikia rūpintis vardikliu, yra tik skaitiklis, kas kombinatorikai itin dėkinga. Iš tiesų, posūkių matricų stulpeliai ir eilutės yra, kaip vektoriai, tampriai susiję. Realiųjų skaičių atveju stulpeliai ir eilutės yra ortonormiški. Užtat ortogonalinės matricos atvirkštinė prilygsta transponuotai matricai. Unitariosios matricos atvirkštinė yra kompleksiškai jungtinė ir transponuota matrica. Supraskime matricos narį kaip taką iš indekso i į indeksą j. Ortogonalinės matricos atveju, atitinkamas atvirkštinės narys išsakys taką atgal iš indekso j į indeksą i. Unitariosios matricos atveju teks papildomai parinkti kompleksišką jungtinę, kas išlaiko skirtumą tarp dviejų krypčių. Simplektinės matricos atveju matricas pasidalina į 2x2 kvadratėlius. Kvadratėlis nusako keturis takus tarp dviejų indeksų turinčių po dvi angas. Du takai veda iš kairės į dešinę ir iš dešinės į kairę. Tiesiog pakeičiame jų kryptį. Likę du takai veda iš kairės į kairę ir iš dešinės į dešinę. Mes taipogi pakeičiame jų kryptį, tačiau taip pat padauginame iš -1, kaip dera skiriant kompleksines jungtines. Tokiu būdu šie keturi takai pasidalina kaip kad kvarternionas pasidalina į du kompleksinius skaičius, nusakančius poziciją ir judesio kiekį, taip kad atvirkštinė išsako kvaternioniškai jungtinę ir transponuotą matricą.
Visa tai apžvelgiant, pastebėkime, kad trikampį galima geometriškai suprasti ir kaip tris takus vedantį ratu, ir kaip tris susikryžiuojančias tieses, ir kaip tris kampus, ir kaip iššluojamą orientuotą plotą. A šeima pagrįsta simpleksais, gimdančius vis naujus takus, griežtai skiriančius židinį kuriame nieko nėra ir visumą, kuriame viskas yra, tad kompleksiniais skaičiais griežtai skiriančius skaičiavimą pirmyn ir skaičiavimą atgal. B šeima pagrįsta kryžminiais politopais, pripažįstančius nulį, gimdančius viršūnių poras, tad ašis, tieses. D šeima pagrįsta hiperkubais, pripažįstančius erdvės visumą, ją skaidančius erdvę į kampus
Posūkių matricos determinantas yra vienas. Tai reiškia, kad Kreimerio taisykle apskaičiuojant atvirkštinę, nereikia rūpintis vardikliu, yra tik skaitiklis, kas kombinatorikai itin dėkinga. Iš tiesų, posūkių matricų stulpeliai ir eilutės yra, kaip vektoriai, tampriai susiję. Realiųjų skaičių atveju stulpeliai ir eilutės yra ortonormiški. Užtat ortogonalinės matricos atvirkštinė prilygsta transponuotai matricai. Unitariosios matricos atvirkštinė yra kompleksiškai jungtinė ir transponuota matrica. Supraskime matricos narį kaip taką iš indekso i į indeksą j. Ortogonalinės matricos atveju, atitinkamas atvirkštinės narys išsakys taką atgal iš indekso j į indeksą i. Unitariosios matricos atveju teks papildomai parinkti kompleksišką jungtinę, kas išlaiko skirtumą tarp dviejų krypčių. Simplektinės matricos atveju matricas pasidalina į 2x2 kvadratėlius. Kvadratėlis nusako keturis takus tarp dviejų indeksų turinčių po dvi angas. Du takai veda iš kairės į dešinę ir iš dešinės į kairę. Tiesiog pakeičiame jų kryptį. Likę du takai veda iš kairės į kairę ir iš dešinės į dešinę. Mes taipogi pakeičiame jų kryptį, tačiau taip pat padauginame iš -1, kaip dera skiriant kompleksines jungtines. Tokiu būdu šie keturi takai pasidalina kaip kad kvarternioną pasidalina į du kompleksinius skaičius, taip kad atvirkštinė išsako kvaternioniškai jungtinė ir transponuota matricą.
Galiausiai, susieti su realiasiais skaičiais, kompleksiniais skaičiais ir kvaternionais. Atvirkštinėmis matricomis.
Gaunasi dvigubai daugiau takų, galima sakyti, porinis skaičius.
Posūkių matricos determinantas yra vienas. Tai reiškia, kad Kreimerio taisykle apskaičiuojant atvirkštinę, nereikia rūpintis vardikliu, yra tik skaitiklis, kas kombinatorikai itin dėkinga. Iš tiesų, posūkių matricų stulpeliai ir eilutės yra, kaip vektoriai, tampriai susiję. Realiųjų skaičių atveju stulpeliai ir eilutės yra ortonormiški. Užtat ortogonalinės matricos atvirkštinė prilygsta transponuotai matricai. Unitariosios matricos atvirkštinė yra kompleksiškai jungtinė ir transponuota matrica. Supraskime matricos narį kaip taką iš indekso i į indeksą j. Ortogonalinės matricos atveju, atitinkamas atvirkštinės narys išsakys taką atgal iš indekso j į indeksą i. Unitariosios matricos atveju teks papildomai parinkti kompleksišką jungtinę, kas išlaiko skirtumą tarp dviejų krypčių. Simplektinės matricos atveju matricas pasidalina į 2x2 kvadratėlius. Kvadratėlis nusako keturis takus tarp dviejų indeksų turinčių po dvi angas. Du takai veda iš kairės į dešinę ir iš dešinės į kairę. Tiesiog pakeičiame jų kryptį. Likę du takai veda iš kairės į kairę ir iš dešinės į dešinę. Mes taipogi pakeičiame jų kryptį, tačiau taip pat padauginame iš -1, kaip dera skiriant kompleksines jungtines. Tokiu būdu šie keturi takai pasidalina kaip kad kvarternionas pasidalina į du kompleksinius skaičius, nusakančius poziciją ir judesio kiekį, taip kad atvirkštinė išsako kvaternioniškai jungtinė ir transponuota matricą.
Posūkių matricos determinantas yra vienas. Tai reiškia, kad Kreimerio taisykle apskaičiuojant atvirkštinę, nereikia rūpintis vardikliu, yra tik skaitiklis, kas kombinatorikai itin dėkinga. Iš tiesų, posūkių matricų stulpeliai ir eilutės yra, kaip vektoriai, tampriai susiję. Realiųjų skaičių atveju stulpeliai ir eilutės yra ortonormiški. Užtat ortogonalinės matricos atvirkštinė prilygsta transponuotai matricai. Unitariosios matricos atvirkštinė yra kompleksiškai jungtinė ir transponuota matrica. Supraskime matricos narį kaip taką iš indekso i į indeksą j. Ortogonalinės matricos atveju, atitinkamas atvirkštinės narys išsakys taką atgal iš indekso j į indeksą i. Unitariosios matricos atveju teks papildomai parinkti kompleksišką jungtinę, kas išlaiko skirtumą tarp dviejų krypčių. Simplektinės matricos atveju
Posūkių matricos determinantas yra vienas. Tai reiškia, kad Kreimerio taisykle apskaičiuojant atvirkštinę, nereikia rūpintis vardikliu, yra tik skaitiklis, kas kombinatorikai itin dėkinga. Iš tiesų, posūkių matricų stulpeliai ir eilutės yra, kaip vektoriai, tampriai susiję. Realiųjų skaičių atveju stulpeliai ir eilutės yra ortonormiški. Užtat ortogonalinės matricos atvirkštinė prilygsta transponuotai matricai. Unitariosios matricos atvirkštinė yra kompleksiškai jungtinė ir transponuota matrica. Supraskime matricos narį kaip taką iš indekso i į indeksą j. Ortogonalinės matricos atveju, atitinkamas atvirkštinės narys išsakys taką atgal iš indekso j į indeksą i. Unitariosios matricos atveju teks papildomai parinkti kompleksišką jungtinę, kas išlaiko skirtumą tarp dviejų krypčių. Simplektinės matricos atveju matricas pasidalina į 2x2 kvadratėlius. Kvadratėlis nusako keturis takus tarp dviejų indeksų turinčių po dvi angas. Du takai veda iš kairės į dešinę ir iš dešinės į kairę. Tiesiog pakeičiame jų kryptį. Likę du takai veda iš kairės į kairę ir iš dešinės į dešinę. Mes taipogi pakeičiame jų kryptį, tačiau taip pat padauginame iš -1, kaip dera skiriant kompleksines jungtines. Tokiu būdu šie keturi takai pasidalina kaip kad kvarternioną pasidalina į du kompleksinius skaičius, taip kad atvirkštinė išsako kvaternioniškai jungtinė ir transponuota matricą.
Posūkių matricos determinantas yra vienas. Tai reiškia, kad Kreimerio taisykle apskaičiuojant atvirkštinę, nereikia rūpintis vardikliu, yra tik skaitiklis, kas kombinatorikai itin dėkinga. Iš tiesų, posūkių matricų stulpeliai ir eilutės yra, kaip vektoriai, tampriai susiję. Realiųjų skaičių atveju stulpeliai ir eilutės yra ortonormiški. Užtat ortogonalinės matricos atvirkštinė prilygsta transponuotai matricai. Unitariosios matricos atvirkštinė yra kompleksiškai jungtinė ir transponuota matrica. Tai reiškia, kad
Posūkių matricos determinantas yra vienas. Tai reiškia, kad Kreimerio taisykle apskaičiuojant atvirkštinę, nereikia rūpintis vardikliu, yra tik skaitiklis, kas kombinatorikai itin dėkinga. Iš tiesų, posūkių matricų stulpeliai ir eilutės yra, kaip vektoriai, tampriai susiję. Realiųjų skaičių atveju stulpeliai ir eilutės yra ortonormiški. Užtat ortogonalinės matricos atvirkštinė prilygsta transponuotai matricai. Unitariosios matricos atvirkštinė yra kompleksiškai jungtinė ir transponuota matrica. Supraskime matricos narį kaip taką iš indekso i į indeksą j. Ortogonalinės matricos atveju, atitinkamas atvirkštinės narys išsakys taką atgal iš indekso j į indeksą i. Unitariosios matricos atveju teks papildomai parinkti kompleksišką jungtinę, kas išlaiko skirtumą tarp dviejų krypčių. Simplektinės matricos atveju
Posūkių matricų determinantai yra vienas. Taikant Kreimerio taisyklę tai reiškia, kad nereikia rūpintis vardikliu, yra tik skaitiklis, kas kombinatorikai itin dėkinga. Iš tiesų, posūkių matricų stulpeliai ir eilutės yra, kaip vektoriai, tampriai susiję. Realųjų skaičių atveju stulpeliai ir eilutės yra ortonormiški. Užtat ortogonalinės matricos atvirkštinė prilygsta transponuotai matricai. Unitariosios matricos atvirkštinė yra kompleksiškai jungtinė ir transponuota matrica. Tai reiškia, kad
Posūkių matricos determinantas yra vienas. Tai reiškia, kad Kreimerio taisykle apskaičiuojant atvirkštinę, nereikia rūpintis vardikliu, yra tik skaitiklis, kas kombinatorikai itin dėkinga. Iš tiesų, posūkių matricų stulpeliai ir eilutės yra, kaip vektoriai, tampriai susiję. Realiųjų skaičių atveju stulpeliai ir eilutės yra ortonormiški. Užtat ortogonalinės matricos atvirkštinė prilygsta transponuotai matricai. Unitariosios matricos atvirkštinė yra kompleksiškai jungtinė ir transponuota matrica. Tai reiškia, kad
Lie teorija yra, mano galvai, siaubingai miglotos bendrybės, tačiau jų išdavos yra stebuklingai dalykiškos. Jų galimybes išsako pavaizduotos Dynkin diagramos. Yra keturios begalinės, klasikinės šeimos ir penkios papildomos išimtys. Mane domina, kaip paprasčiausiai suprasti ir paaiškinti, kuomi pasižymi šios klasikinės šeimos ir kodėl jų yra būtent keturios.
Lie teorija yra, mano galvai, siaubingai miglotos bendrybės, tačiau jos išdavos yra stebuklingai dalykiškos. Galimybes išsako pavaizduotos Dynkin diagramos. Yra keturios begalinės, klasikinės šeimos ir penkios papildomos išimtys. Mane domina, kaip paprasčiausiai suprasti ir paaiškinti, kuomi pasižymi šios klasikinės šeimos ir kodėl jų yra būtent keturios.
Įdomu, kad panašūs takai įžvelgtini interpretuojant Lie grupių matricų atvirkštines. Lie grupių matricos išsako posūkius, tad jų determinantai yra vienas, ir taikant Kreimerio taisyklę tai reiškia, kad nereikia rūpintis vardikliu, yra tik skaitiklis, kas kombinatorikai itin dėkinga. Iš tiesų, posūkių matricų stulpeliai ir eilutės yra, kaip vektoriai, tampriai susiję. Realųjų skaičių atveju stulpeliai ir eilutės yra ortonormiški. Iš to kyla, kad ortogonalinės matricos atvirkštinė prilygsta transponuotai matricai. Kompleksinių skaičių atveju, unitarinės matricos atvirkštinė prilygsta
Įdomu, kad panašūs takai įžvelgtini interpretuojant Lie grupių matricų atvirkštines. Lie grupių matricos išsako posūkius. Ortogonalinės matricos nusako posūkius realiųjų skaičių erdvėje. D šeimai priklauso porinių dimensijų ortogonalinės matricos, o B šeimai priklauso neporinių dimensijų. Poriškumas ir neporiškumas iškyla dėl to nuliaus nebuvimo ar buvimo. A šeimai priklauso unitariosios matricos, nusakančios posūkius kompleksinių skaičių erdvėje. C šeimai priklauso simplektinės matricos, nusakančios posūkius kvaternionų erdvėje.
Posūkių matricų determinantai yra vienas. Taikant Kreimerio taisyklę tai reiškia, kad nereikia rūpintis vardikliu, yra tik skaitiklis, kas kombinatorikai itin dėkinga. Iš tiesų, posūkių matricų stulpeliai ir eilutės yra, kaip vektoriai, tampriai susiję. Realųjų skaičių atveju stulpeliai ir eilutės yra ortonormiški. Užtat ortogonalinės matricos atvirkštinė prilygsta transponuotai matricai. Unitariosios matricos atvirkštinė yra kompleksiškai jungtinė ir transponuota matrica. Tai reiškia, kad
Įdomu, kad panašūs takai įžvelgtini Lie grupių matricas ir jų atvirkšties. Lie grupių matricos išsako posūkius, jų determinantai yra vienas, ir pagal Kreimerio taisyklę tai reiškia, kad atvirkštinių nariai nėra trupmenos, kas
Įdomu, kad panašūs takai įžvelgtini interpretuojant Lie grupių matricų atvirkštines. Lie grupių matricos išsako posūkius, tad jų determinantai yra vienas, ir taikant Kreimerio taisyklę tai reiškia, kad nereikia rūpintis vardikliu, yra tik skaitiklis, kas kombinatorikai itin dėkinga. Iš tiesų, posūkių matricų stulpeliai ir eilutės yra, kaip vektoriai, tampriai susiję. Realųjų skaičių atveju stulpeliai ir eilutės yra ortonormiški. Iš to kyla, kad ortogonalinės matricos atvirkštinė prilygsta transponuotai matricai. Kompleksinių skaičių atveju, unitarinės matricos atvirkštinė prilygsta
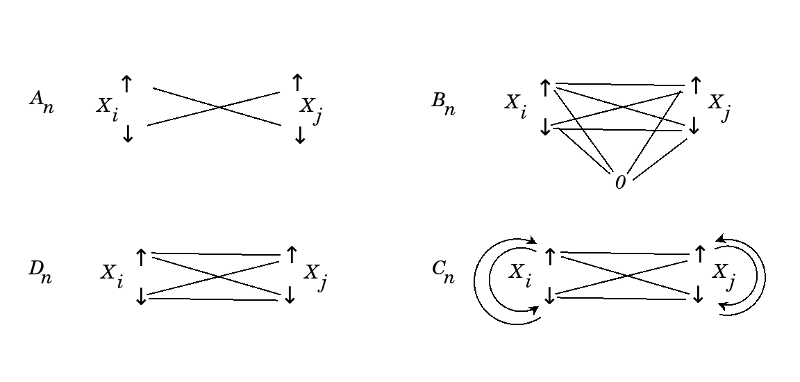
Dabar pasižiūrėkime į šias šaknų sistemas truputį kitaip ir suprasime kaip jos atitinka keturias sandaugų simetrijas. Įsivaizduokime, kad kiekvienas indeksas turi dvi angas, kairę ir dešinę. Šaknį galime laikyti taku tarp dviejų indeksų. A šeima griežtai skiria angas, taip kad vieni takai keliauja iš kairės į dešinę, o kiti takai keliauja iš dešinės į kairę. D šeima neskiria angų, taip kad galima keliauti iš kairės į kairę, iš kairės į dešinę, iš dešinės į kairę, ir iš dešinės į dešinę. B šeima yra panaši, tik jinai dar ir takus iš kiekvieno nario kairę į nulį. Nulio kairė ir dešinė sutampa, tad sutampa atitinkantys takai. Galiausiai C šeima yra panaši į D šeimą, tik jinai prideda taškus iš kiekvieno nario kairę į savo dešinę, ir iš kiekvieno nario dešinę į savo kairę. Gaunasi dvigubai daugiau takų, galima sakyti, porinis skaičius.
Dabar pasižiūrėkime į šias šaknų sistemas truputį kitaip ir suprasime kaip jos atitinka keturias sandaugų simetrijas. Įsivaizduokime, kad kiekvienas indeksas turi dvi angas, kairę ir dešinę. Šaknį galime laikyti taku tarp dviejų indeksų. A šeima griežtai skiria angas, taip kad vieni takai keliauja iš kairės į dešinę, o kiti takai keliauja iš dešinės į kairę. D šeima neskiria angų, taip kad galima keliauti iš kairės į kairę, iš kairės į dešinę, iš dešinės į kairę, ir iš dešinės į dešinę. B šeima yra panaši, tik jinai dar ir takus iš kiekvieno nario kairę į nulį. Nulio kairė ir dešinė sutampa, tad sutampa atitinkantys takai. Galiausiai C šeima yra panaši į D šeimą, tik jinai prideda taškus iš kiekvieno nario kairę į savo dešinę, ir iš kiekvieno nario dešinę į savo kairę. Užtat būtent C šeimoje einant tokiu iš nario į save apsisuka skaičiavimo kryptis. Tuo tarpu A šeimoje skaičiavimo kryptys griežtai skiriamos, o B ir D šeimose jos neskiriamos.
Įdomu, kad panašūs takai įžvelgtini Lie grupių matricas ir jų atvirkšties. Lie grupių matricos išsako posūkius, jų determinantai yra vienas, ir pagal Kreimerio taisyklę tai reiškia, kad atvirkštinių nariai nėra trupmenos, kas
Gaunasi dvigubai daugiau takų, galima sakyti, porinis skaičius.
Dabar pasižiūrėkime į šias šaknų sistemas truputį kitaip ir suprasime kaip jos atitinka keturias sandaugų simetrijas. Įsivaizduokime, kad kiekvienas indeksas turi dvi angas, kairę ir dešinę. Šaknį galime laikyti taku tarp dviejų indeksų. A šeima griežtai skiria angas, taip kad vieni takai keliauja iš kairės į dešinę, o kiti takai keliauja iš dešinės į kairę. D šeima neskiria angų, taip kad galima keliauti iš kairės į kairę, iš kairės į dešinę, iš dešinės į kairę, ir iš dešinės į dešinę. B šeima yra panaši, tik jinai dar prideda takus iš kiekvieno nario į nulį, teturintį vieną angą. Gaunasi dvigubai daugiau takų, galima sakyti, porinis skaičius.
Dabar pasižiūrėkime į šias šaknų sistemas truputį kitaip ir suprasime kaip jos atitinka keturias sandaugų simetrijas. Įsivaizduokime, kad kiekvienas indeksas turi dvi angas, kairę ir dešinę. Šaknį galime laikyti taku tarp dviejų indeksų. A šeima griežtai skiria angas, taip kad vieni takai keliauja iš kairės į dešinę, o kiti takai keliauja iš dešinės į kairę. D šeima neskiria angų, taip kad galima keliauti iš kairės į kairę, iš kairės į dešinę, iš dešinės į kairę, ir iš dešinės į dešinę. B šeima yra panaši, tik jinai dar ir takus iš kiekvieno nario kairę į nulį. Nulio kairė ir dešinė sutampa, tad sutampa atitinkantys takai. Galiausiai C šeima yra panaši į D šeimą, tik jinai prideda taškus iš kiekvieno nario kairę į savo dešinę, ir iš kiekvieno nario dešinę į savo kairę. Gaunasi dvigubai daugiau takų, galima sakyti, porinis skaičius.
Dabar pasižiūrėkime į šias šaknų sistemas truputį kitaip ir suprasime kaip jos atitinka keturias sandaugų simetrijas. Įsivaizduokime, kad kiekvienas indeksas turi dvi angas, kairę ir dešinę. Šaknį galime laikyti taku tarp dviejų indeksų. A šeima griežtai skiria angas, taip kad vieni takai keliauja iš kairės į dešinę, o kiti takai keliauja iš dešinės į kairę. D šeima neskiria angų, taip kad galima keliauti iš kairės į kairę, iš kairės į dešinę, iš dešinės į kairę, ir iš dešinės į dešinę. B šeima yra panaši, tik jinai dar prideda takus iš Gaunasi dvigubai daugiau takų, galima sakyti, porinis skaičius.
Dabar pasižiūrėkime į šias šaknų sistemas truputį kitaip ir suprasime kaip jos atitinka keturias sandaugų simetrijas. Įsivaizduokime, kad kiekvienas indeksas turi dvi angas, kairę ir dešinę. Šaknį galime laikyti taku tarp dviejų indeksų. A šeima griežtai skiria angas, taip kad vieni takai keliauja iš kairės į dešinę, o kiti takai keliauja iš dešinės į kairę. D šeima neskiria angų, taip kad galima keliauti iš kairės į kairę, iš kairės į dešinę, iš dešinės į kairę, ir iš dešinės į dešinę. B šeima yra panaši, tik jinai dar prideda takus iš kiekvieno nario į nulį, teturintį vieną angą. Gaunasi dvigubai daugiau takų, galima sakyti, porinis skaičius.
Dabar pasižiūrėkime į šias šaknų sistemas truputį kitaip ir suprasime kaip jos atitinka keturias sandaugų simetrijas. Įsivaizduokime, kad kiekvienas indeksas turi dvi angas, kairę ir dešinę. Šaknį galime laikyti taku tarp dviejų indeksų. A šeima griežtai skiria angas, taip kad vieni takai keliauja iš kairės į dešinę, o kiti takai keliauja iš dešinės į kairę. D šeima neskiria angų, taip kad galima keliauti iš kairės į kairę, iš kairės į dešinę, iš dešinės į kairę, ir iš dešinės į dešinę. Gaunasi dvigubai daugiau takų, galima sakyti, porinis skaičius. B šeima yra panaši, tik jinai dar prideda takus iš
Įsidėkime takus iš vieno indekso į kitą indeksą. A šeima tais takais tarsi keliauja elektronai ir positronai, griežtai skiriantys teigiamumą ir neigiamumą. Elektronai keliauja iš neigiamo į teigiamą, o positronai keliauja iš teigiamo į neigiamą. D šeima sunivel
Dabar pasižiūrėkime į šias šaknų sistemas truputį kitaip ir suprasime kaip jos atitinka keturias sandaugų simetrijas. Įsivaizduokime, kad kiekvienas indeksas turi dvi angas, kairę ir dešinę. Šaknį galime laikyti taku tarp dviejų indeksų. A šeima griežtai skiria angas, taip kad vieni takai keliauja iš kairės į dešinę, o kiti takai keliauja iš dešinės į kairę. D šeima neskiria angų, taip kad galima keliauti iš kairės į kairę, iš kairės į dešinę, iš dešinės į kairę, ir iš dešinės į dešinę. B šeima yra panaši, tik jinai dar prideda takus iš Gaunasi dvigubai daugiau takų, galima sakyti, porinis skaičius.
Dabar pasižiūrėkime į šias šaknų sistemas truputį kitaip ir suprasime kaip jos atitinka keturias sandaugų simetrijas. Įsidėkime takus iš vieno indekso į kitą indeksą. A šeima tais takais tarsi keliauja elektronai ir positronai, griežtai skiriantys teigiamumą ir neigiamumą. Elektronai keliauja iš neigiamo į teigiamą, o positronai keliauja iš teigiamo į neigiamą. D šeima sunivel
Dabar pasižiūrėkime į šias šaknų sistemas truputį kitaip ir suprasime kaip jos atitinka keturias sandaugų simetrijas. Įsivaizduokime, kad kiekvienas indeksas turi dvi angas, kairę ir dešinę. Šaknį galime laikyti taku tarp dviejų indeksų. A šeima griežtai skiria angas, taip kad vieni takai keliauja iš kairės į dešinę, o kiti takai keliauja iš dešinės į kairę. D šeima neskiria angų, taip kad galima keliauti iš kairės į kairę, iš kairės į dešinę, iš dešinės į kairę, ir iš dešinės į dešinę. Gaunasi dvigubai daugiau takų, galima sakyti, porinis skaičius. B šeima yra panaši, tik jinai dar prideda takus iš
Įsidėkime takus iš vieno indekso į kitą indeksą. A šeima tais takais tarsi keliauja elektronai ir positronai, griežtai skiriantys teigiamumą ir neigiamumą. Elektronai keliauja iš neigiamo į teigiamą, o positronai keliauja iš teigiamo į neigiamą. D šeima sunivel
Dabar pasižiūrėkime į šias šaknų sistemas truputį kitaip ir suprasime kaip jos atitinka keturias sandaugų simetrijas. Įsidėkime takus iš vieno indekso į kitą indeksą. A šeima tais takais tarsi keliauja elektronai ir positronai, griežtai skiriantys teigiamumą ir neigiamumą. Elektronai keliauja iš neigiamo į teigiamą, o positronai keliauja iš teigiamo į neigiamą.
Dabar pasižiūrėkime į šias šaknų sistemas truputį kitaip ir suprasime kaip jos atitinka keturias sandaugų simetrijas. Įsidėkime takus iš vieno indekso į kitą indeksą. A šeima tais takais tarsi keliauja elektronai ir positronai, griežtai skiriantys teigiamumą ir neigiamumą. Elektronai keliauja iš neigiamo į teigiamą, o positronai keliauja iš teigiamo į neigiamą. D šeima sunivel
Visa tai turint omenyje, dabar paaiškinsiu, kaip galima suprasti klasikinių Lie algebrų šaknų sistemas. Galime jų paprastasias šaknis {$x_2-x_1$}, {$x_3-x_2$} ir taip toliau suprasti, kaip koduojančius skaičiavimą, 1, 2, 3 ir toliau iki skaičaus n. A šeima skaičiuoja toliau, {$x_{n+1}-x_n$}. Įsidėmėkime, yra dualizmas, kuriuo iš vieno galo skaičiuodami pirmyn 1, 2, 3 tuo pačiu iš kito galo skaičiuojame atgal -3, -2, -1. Ir įsivaizduokime, kaip senovės istorikams teko susitarti, kaip sudurti metų skaičiavimą pirmyn mūsų eroje su metų skaičiavimu atgal prieš mūsų erą. Tad trys klasikinės šeimos skirtingais būdais sprendžia, kaip sieti tokias dvi skaičiavimo kryptis. B šeima įveda papildomą, išorinį nulį, tuštumą, {$x_0=0$}, taip kad skaičiavimas vyksta -2, -1, 0, 1, 2. Pereinama iš 0 į 1, užtat atsiranda papildoma šaknis {$x_1-x_0=x_1$}. D šeima apibrėžia vidinį nulį sutapatinant -1 ir 1, taip kad skaičiavimas vyksta -3, -2, -1=1, 2, 3. Pereinama iš -2 į 1, užtat atsiranda papildoma šaknis {$x_1-(-x_2)=x_1+x_2$}. O C šeima tiesiog suduria abu skaičiavimus: -2, -1, 1, 2. Pereinama iš -1 į 1 užtat atsiranda papildoma šaknis {$x_1-(-x_1)=2x_1$}.
Visa tai turint omenyje, dabar paaiškinsiu, kaip galima suprasti klasikinių Lie algebrų šaknų sistemas. Galime jų paprastasias šaknis {$x_2-x_1$}, {$x_3-x_2$} ir taip toliau suprasti, kaip koduojančius skaičiavimą, 1, 2, 3 ir toliau iki skaičaus n. A šeima skaičiuoja toliau, {$x_{n+1}-x_n$}. Įsidėmėkime, yra dualizmas, kuriuo iš vieno galo skaičiuodami pirmyn 1, 2, 3 tuo pačiu iš kito galo skaičiuojame atgal -3, -2, -1. Ir įsivaizduokime, kaip senovės istorikams teko susitarti, kaip sudurti metų skaičiavimą pirmyn mūsų eroje su metų skaičiavimu atgal prieš mūsų erą. Tad trys klasikinės šeimos skirtingais būdais sprendžia, kaip sieti tokias dvi skaičiavimo kryptis. B šeima įveda papildomą, išorinį nulį, tuštumą, {$x_0=0$}, taip kad skaičiavimas vyksta -2, -1, 0, 1, 2. Pereinama iš 0 į 1, užtat atsiranda papildoma šaknis {$x_1-x_0=x_1$}. Galime įsivaizduoti, kad siūlo galus pririšome prie to išorinio nulio. D šeima apibrėžia vidinį nulį sutapatinant -1 ir 1, taip kad skaičiavimas vyksta -3, -2, -1=1, 2, 3. Pereinama iš -2 į 1, užtat atsiranda papildoma šaknis {$x_1-(-x_2)=x_1+x_2$}. Siūlo galus sulydėme. O C šeima tiesiog suduria abu skaičiavimus: -2, -1, 1, 2. Pereinama iš -1 į 1 užtat atsiranda papildoma šaknis {$x_1-(-x_1)=2x_1$}. Galima sakyti, siūlą tiesiog sulankstėme.
Dabar pasižiūrėkime į šias šaknų sistemas truputį kitaip ir suprasime kaip jos atitinka keturias sandaugų simetrijas.
Dabar pasižiūrėkime į šias šaknų sistemas truputį kitaip ir suprasime kaip jos atitinka keturias sandaugų simetrijas. Įsidėkime takus iš vieno indekso į kitą indeksą. A šeima tais takais tarsi keliauja elektronai ir positronai, griežtai skiriantys teigiamumą ir neigiamumą. Elektronai keliauja iš neigiamo į teigiamą, o positronai keliauja iš teigiamo į neigiamą.
Lie teorija yra, mano galvai, siaubingai miglotos bendrybės, tačiau jų išdavos yra netikėtai dalykiškos. Jų galimybes išsako pavaizduotos Dynkin diagramos. Yra keturios begalinės, klasikinės šeimos ir penkios papildomos išimtys. Mane domina, kaip paprasčiausiai suprasti ir paaiškinti, kuomi pasižymi šios klasikinės šeimos ir kodėl jų yra būtent keturios.
Lie teorija yra, mano galvai, siaubingai miglotos bendrybės, tačiau jų išdavos yra stebuklingai dalykiškos. Jų galimybes išsako pavaizduotos Dynkin diagramos. Yra keturios begalinės, klasikinės šeimos ir penkios papildomos išimtys. Mane domina, kaip paprasčiausiai suprasti ir paaiškinti, kuomi pasižymi šios klasikinės šeimos ir kodėl jų yra būtent keturios.
Gyvenime nesimetriškos priešingybės pavyzdys yra būti ar nebūti, o simetriškos priešingybės pavyzdys yra būti vienokiu ar būti kitokiu. Ši plonybė pasireiškia mąstant kintamųjų sandaugas, jas modeliuojant binomo teorema, Paskalio trikampiu, ir skirtingai interpruojant politopais.
Jeigu nori, kad mergytė valgytų, turi jai duoti simetrišką pasirinkimą: ar nori valgyti dešrelę ar bananą? Jeigu paklausi nesimetriškai, ar nori valgyti? tai gali visai nevalgyti. Jeigu neturi pinigų, tai rašyk nulį, o tai bus simetriška milijonui. O jeigu nieko nerašysi, tai tavo nulis bus nesimetriškas tam milijonui. Būti ar nebūti yra nesimetriška priešingybė, būti vienokiu ar kitokiu yra simetriška priešingybė. Ši plonybė pasireiškia mąstant kintamųjų sandaugas, jas modeliuojant binomo teorema, Paskalio trikampiu, ir skirtingai interpruojant politopais.
Kryžminio politopų dualas yra hiperkubai. Tos
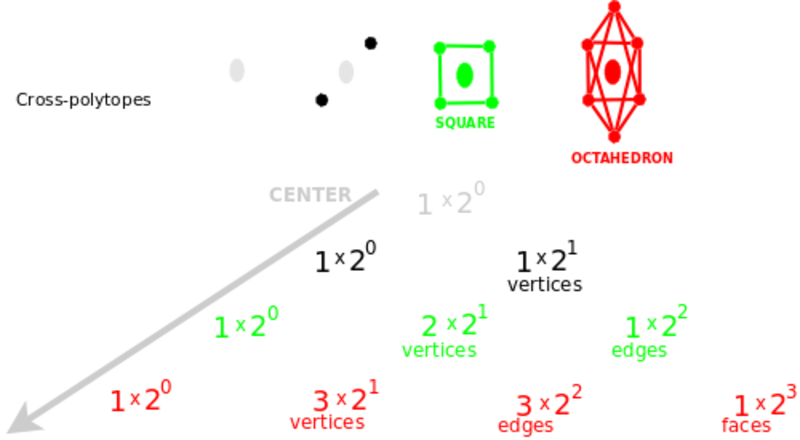
Kryžminiai politopai ir kubai. Židinys ir visuma.
Keturios galimybės, kaip protui nusiteikti:
- išsirinkti ar neišsirinkti
- išsirinkti vienaip ar išsirinkti kitaip ar neišsirinkti
- išsirinkti ar neišsirinkti vienaip ar neišsirinkti kitaip
- išsirinkti vienaip ar išsirinkti kitaip = neišsirinkti vienaip ar neišsirinkti kitaip
Yra tokios grynos galimybės iš kurių toliau gali būti suduriamos mišrios galimybės.
Politopai.
Skaičiavimas: 1, 2, 3, ... yra tuo pačiu -3, -2, -1. Galima susieti abu skaičiavimus.
Kryžminio politopų dualas yra hiperkubai. Hiperkubas susidaro iš erdvės skaidymų. Pavyzdžiui, kubas turi vieną visumą, tris kart du šonus, tris kart keturias kraštines, ir aštuonias viršūnes. Užtat viską skaidantis hiperkubas neturi židinio.
Viską apžvelgus, besirenkantis protas gali ketveriopai nusiteikti:
- simpleksais: išsirinkti ar neišsirinkti
- kryžminiais politopais: išsirinkti vienaip ar išsirinkti kitaip ar neišsirinkti
- hiperkubais: išsirinkti ar neišsirinkti vienaip ar neišsirinkti kitaip
- koordinačių sistemomis: išsirinkti vienaip ar išsirinkti kitaip - arba tolygiai - neišsirinkti vienaip ar neišsirinkti kitaip
Kryžminio politopų dua
Kryžminio politopų dualas yra hiperkubai. Tos
Simetriškas priešingybes vaizduoja koordinačių sistemos. Koordinates išsakysiu strėlėmis, į kairę ir į dešinę, kad jų simetriškumas būtų akivaizdus. Kubo aštuonios viršūnės išsidėsto pagal Paskalio trikampį. Kubą galime atitinkamai supjaustyti. Šitaip mąstant kubas nėra politopas, jis nesusideda iš politopų, nėra židinio, nė visumos. Šio kūbo viršūnės yra savybių rinkiniai, kad kiekvienu klausimu, kiekviename mate, pasirinkta vienaip arba kitaip. Užtat sukeitus visas strėles į kairę ir į dešinę niekas iš esmės nepasikeistų, nes tai iš tiesų tėra semantinis skirtumas, priklausantis nuo visuminio konteksto, ką reiškia strėlė į kairę ir strėlė į dešinę.
Simetriškas priešingybes vaizduoja koordinačių sistemos. Koordinates išsakysiu strėlėmis, į kairę ir į dešinę, kad jų simetriškumas būtų akivaizdus. Kubo aštuonios viršūnės išsidėsto pagal Paskalio trikampį. Kubą galime atitinkamai supjaustyti. Šitaip mąstant kubas nėra politopas, jis nesusideda iš politopų, nėra židinio, nė visumos. Šis kūbas susideda iš ašių, tad jo viršūnės yra savybių rinkiniai. Kiekvienu klausimu, kiekviename mate, kiekvienoje ašyje pasirinkta vienaip arba kitaip. Užtat sukeitus visas strėles į kairę ir į dešinę niekas iš esmės nepasikeistų, nes tai iš tiesų tėra semantinis skirtumas, priklausantis nuo visuminio konteksto, ką reiškia strėlė į kairę ir strėlė į dešinę. Užtat tokios koordinačių sistemos simetrijų grupę tenka padalinti iš dviejų. Simplekso simetrijas išsako simetrinė grupė, o koordinačių sistemos simetrijas išsako alternatyvi grupė.
Yra dar du mišrūs pasirinkimai, kuriuos išsako kryžminiai politopai ir hiperkubai.
Yra dar du mišrūs pasirinkimai, kuriuos išsako kryžminiai politopai ir hiperkubai. Įsivaizduokime, kad židinys gimdo viršūnes poromis, tarsi teigiamas ir neigiamas dalelytes, skriejančias priešingomis kryptimis, ištiesiančias ašis arba tieses. Tuomet Paskalio trikampį galima suvokti, kaip siejantį ašis. Oktahedrą sudaro trys ašys. Jisai turi vieną židinį, tris kart du, tai yra, šešias viršūnes, tris kart keturias, tai yra, dvylika kraštinių, ir aštuonis šonus. Įsidėmėkime, kad Paskalio trikampis tvirtina, kad oktahedras neturi visumos, neturi tūrio! Užtat jisai turi aštuonis orientuotus šonus, kuriais skiria vidų ir išorę.
Kryžminio politopų dua
Koordinačių sistemos.
Kvantinei fizikos šios plonybės turėtų būti svarbios.
Simetriškas priešingybes vaizduoja koordinačių sistemos. Koordinates išsakysiu strėlėmis, į kairę ir į dešinę, kad jų simetriškumas būtų akivaizdus. Kubo aštuonios viršūnės išsidėsto pagal Paskalio trikampį. Kubą galime atitinkamai supjaustyti. Šitaip mąstant kubas nėra politopas, jis nesusideda iš politopų, nėra židinio, nė visumos. Šio kūbo viršūnės yra savybių rinkiniai, kad kiekvienu klausimu, kiekviename mate, pasirinkta vienaip arba kitaip. Užtat sukeitus visas strėles į kairę ir į dešinę niekas iš esmės nepasikeistų, nes tai iš tiesų tėra semantinis skirtumas, priklausantis nuo visuminio konteksto, ką reiškia strėlė į kairę ir strėlė į dešinę.
Kvantinei fizikos šios plonybės turėtų būti svarbios nes jos skiria stebinį ir stebėtoją. Gamtoje visada būna arba vienaip arba kitaip. Gamtoje tarpų nebūna. O stebėtoja stebi, kas įvyks tam tikru metu, jinai atrėžia stebėjimo tarpus. Stebėjimo tarpe gali kažkas įvykti arba neįvykti, būti arba nebūti. Stebėtojas plėtoja nesimetriškas priešingybes, o stebinys plėtoja simetriškas priešingybes.
Yra dar du mišrūs pasirinkimai, kuriuos išsako kryžminiai politopai ir hiperkubai.
Viena politopų šeima yra simpleksai, kuriuos galime generuoti taip. Pradėkime nuo tuščio židinio ir duokime tam židiniui vis pagimdyti po vieną viršūnę. Viena viršūnė, tai taškas. Iš židinio išskiriant antrą viršūnę, gauname tiesės atkarpą, ir židinys pasislenka. Pagimdžius trečią viršūnę išvystame trikampį, pagimždius ketvirtą viršūnę - tetrahedrą su keturiais trikampiniais šoniais. Paskalio trikampis atskleidžia iš ko šie simpleksai susideda. Trikampis turi vieną židinį, tris viršūnes, tris kraštines ir vieną visumą. Tetrahedras turi vieną židinį, keturias viršūnes, šešias kraštines, keturis šonus ir vieną visumą. Ir jeigu savo vaizduote patampytumėme tetrahedro židinį, įsitikintumėme, kad ketvirtamatis simpleksas susidarys iš vieno židinio, penkių viršūnių, dešimt kraštinių, dešimt šonų, penkių tetrahedrų ir vienos visumos.
Viena politopų šeima yra simpleksai, kuriuos galime generuoti taip. Pradėkime nuo tuščio židinio ir duokime tam židiniui vis pagimdyti po vieną viršūnę. Viena viršūnė, tai taškas. Iš židinio išskiriant antrą viršūnę, gauname tiesės atkarpą, ir židinys pasislenka. Pagimdžius trečią viršūnę išvystame trikampį, pagimždius ketvirtą viršūnę - tetrahedrą su keturiais trikampiniais šoniais. Paskalio trikampis atskleidžia iš ko šie simpleksai susideda. Trikampis turi vieną židinį, tris viršūnes, tris kraštines ir vieną visumą. Tetrahedras turi vieną židinį, keturias viršūnes, šešias kraštines, keturis šonus ir vieną visumą. Ir jeigu savo vaizduote patampytumėme tetrahedro židinį, įsitikintumėme, kad ketvirtamatis simpleksas susidarys iš vieno židinio, penkių viršūnių, dešimt kraštinių, dešimt šonų, penkių tetrahedrų ir vienos visumos. Noriu atkreipti dėmesį, kad kiekviename simplekse, pavyzdžiui, trikampyje, židinys ir visuma yra nesimetriškos priešingybės, mat, židinys susidaro iš jokių viršūnių, o visuma susidaro iš visų viršūnių. Tai yra ne šiaip semantinis skirtumas, kaip ką pavadiname, o sintaktinis skirtumas tarp to kas yra ir to ko visiškai nėra.
Kvantinei fizikos šios plonybės turėtų būti svarbios.
Viena politopų šeima yra simpleksai, kuriuos galime generuoti taip. Pradėkime nuo tuščio židinio ir duokime tam židiniui vis pagimdyti po vieną viršūnę. Viena viršūnė, tai taškas. Antra
Viena politopų šeima yra simpleksai, kuriuos galime generuoti taip. Pradėkime nuo tuščio židinio ir duokime tam židiniui vis pagimdyti po vieną viršūnę. Viena viršūnė, tai taškas. Iš židinio išskiriant antrą viršūnę, gauname tiesės atkarpą, ir židinys pasislenka. Pagimdžius trečią viršūnę išvystame trikampį, pagimždius ketvirtą viršūnę - tetrahedrą su keturiais trikampiniais šoniais. Paskalio trikampis atskleidžia iš ko šie simpleksai susideda. Trikampis turi vieną židinį, tris viršūnes, tris kraštines ir vieną visumą. Tetrahedras turi vieną židinį, keturias viršūnes, šešias kraštines, keturis šonus ir vieną visumą. Ir jeigu savo vaizduote patampytumėme tetrahedro židinį, įsitikintumėme, kad ketvirtamatis simpleksas susidarys iš vieno židinio, penkių viršūnių, dešimt kraštinių, dešimt šonų, penkių tetrahedrų ir vienos visumos.
Galiausiai, susieti su realiasiais skaičiais, kompleksiniais skaičiais ir kvaternionais.
Galiausiai, susieti su realiasiais skaičiais, kompleksiniais skaičiais ir kvaternionais. Atvirkštinėmis matricomis.
Išmąsčiau, kad keturios klasikinės šeimos išsako simetrijas slypiančias pačioje matematikoje, tai yra, bet kurioje sandaugoje, bet kurioje pasirinkimų grandinėje. Pristatysiu keturis skirtingus būdus, kaip galime mąstyti pasirinkimų grandinę.
Išmąsčiau, kad keturios klasikinės šeimos išsako simetrijas slypiančias pačioje matematikoje, tai yra, glūdinčios mąstant bet kurią sandaugą, bet kurią pasirinkimų grandinę. Pristatysiu keturis skirtingus būdus, kaip galime mąstyti pasirinkimų grandinę.
Lie teorija yra, mano galvai, siaubingai abstrakti, tačiau jos išdavos yra netikėtai dalykiškos. Jų galimybes išsako pavaizduotos Dynkin diagramos. Yra keturios begalinės, klasikinės šeimos ir penkios papildomos išimtys. Mane domina, kaip paprasčiausiai suprasti ir paaiškinti, kuomi pasižymi šios klasikinės šeimos ir kodėl jų yra būtent keturios.
Lie teorija yra, mano galvai, siaubingai miglotos bendrybės, tačiau jų išdavos yra netikėtai dalykiškos. Jų galimybes išsako pavaizduotos Dynkin diagramos. Yra keturios begalinės, klasikinės šeimos ir penkios papildomos išimtys. Mane domina, kaip paprasčiausiai suprasti ir paaiškinti, kuomi pasižymi šios klasikinės šeimos ir kodėl jų yra būtent keturios.
Lie teorija yra, mano manymu, siaubingai abstrakti, tačiau jos išdavos yra netikėtai dalykiškos. Jų galimybes išsako pavaizduotos Dynkin diagramos. Yra keturios begalinės, klasikinės šeimos ir penkios papildomos išimtys. Mane domina, kaip paprasčiausiai suprasti ir paaiškinti, kuomi pasižymi šios klasikinės šeimos ir kodėl jų yra būtent keturios.
Lie teorija yra, mano galvai, siaubingai abstrakti, tačiau jos išdavos yra netikėtai dalykiškos. Jų galimybes išsako pavaizduotos Dynkin diagramos. Yra keturios begalinės, klasikinės šeimos ir penkios papildomos išimtys. Mane domina, kaip paprasčiausiai suprasti ir paaiškinti, kuomi pasižymi šios klasikinės šeimos ir kodėl jų yra būtent keturios.
Dabar pasižiūrėkime į šias šaknų sistemas truputį kitaip ir suprasime kaip jos atitinka keturias sandaugų simetrijas.
Galiausiai, susieti su realiasiais skaičiais, kompleksiniais skaičiais ir kvaternionais.
Visa tai turint omenyje, dabar paaiškinsiu, kaip galima suprasti klasikinių Lie algebrų šaknų sistemas. Galime jų paprastasias šaknis {$x_2-x_1$}, {$x_3-x_2$} ir taip toliau suprasti, kaip koduojančius skaičiavimą, 1, 2, 3 ir toliau iki skaičaus n. A šeima skaičiuoja toliau, {$x_{n+1}-x_n$}. Įsidėmėkime, yra dualizmas, kuriuo iš vieno galo skaičiuodami pirmyn 1, 2, 3 tuo pačiu iš kito galo skaičiuojame atgal -3, -2, -1. Kitos trys šeimos skirtingais būdais susieja šias dvi skaičiavimo kryptis. B šeima įveda papildomą, išorinį nulį, tuštumą, {$x_0=0$}, taip kad skaičiavimas vyksta -2, -1, 0, 1, 2. Pereinama iš 0 į 1, užtat atsiranda papildoma šaknis {$x_1-x_0=x_1$}. D šeima apibrėžia vidinį nulį sutapatinant -1 ir 1, taip kad skaičiavimas vyksta -3, -2, -1=1, 2, 3. Pereinama iš -2 į 1, užtat atsiranda papildoma šaknis {$x_1-(-x_2)=x_1+x_2$}. O C šeima tiesiog suduria abu skaičiavimus: -2, -1, 1, 2. Pereinama iš -1 į 1 užtat atsiranda papildoma šaknis {$x_1-(-x_1)=2x_1$}.
Visa tai turint omenyje, dabar paaiškinsiu, kaip galima suprasti klasikinių Lie algebrų šaknų sistemas. Galime jų paprastasias šaknis {$x_2-x_1$}, {$x_3-x_2$} ir taip toliau suprasti, kaip koduojančius skaičiavimą, 1, 2, 3 ir toliau iki skaičaus n. A šeima skaičiuoja toliau, {$x_{n+1}-x_n$}. Įsidėmėkime, yra dualizmas, kuriuo iš vieno galo skaičiuodami pirmyn 1, 2, 3 tuo pačiu iš kito galo skaičiuojame atgal -3, -2, -1. Ir įsivaizduokime, kaip senovės istorikams teko susitarti, kaip sudurti metų skaičiavimą pirmyn mūsų eroje su metų skaičiavimu atgal prieš mūsų erą. Tad trys klasikinės šeimos skirtingais būdais sprendžia, kaip sieti tokias dvi skaičiavimo kryptis. B šeima įveda papildomą, išorinį nulį, tuštumą, {$x_0=0$}, taip kad skaičiavimas vyksta -2, -1, 0, 1, 2. Pereinama iš 0 į 1, užtat atsiranda papildoma šaknis {$x_1-x_0=x_1$}. D šeima apibrėžia vidinį nulį sutapatinant -1 ir 1, taip kad skaičiavimas vyksta -3, -2, -1=1, 2, 3. Pereinama iš -2 į 1, užtat atsiranda papildoma šaknis {$x_1-(-x_2)=x_1+x_2$}. O C šeima tiesiog suduria abu skaičiavimus: -2, -1, 1, 2. Pereinama iš -1 į 1 užtat atsiranda papildoma šaknis {$x_1-(-x_1)=2x_1$}.
Palyginkime klasikinių Lie algebrų šaknų sistemas. Galime jų paprastasias šaknis {$x_2-x_1$}, {$x_3-x_2$} ir taip toliau suprasti, kaip koduojančius skaičiavimą, 1, 2, 3 ir toliau iki skaičaus n. A šeima skaičiuoja toliau, {$x_{n+1}-x_n$}. Iš tikrųjų, yra dualizmas, kuriuo iš vieno galo skaičiuodami pirmyn 1, 2, 3 tuo pačiu iš kito galo skaičiuojame atgal -3, -2, -1. Kitos trys šeimos skirtingais būdais susieja šias dvi skaičiavimo kryptis. B šeima įveda papildomą, išorinį nulį, tuštumą, {$x_0=0$}, taip kad skaičiavimas vyksta -2, -1, 0, 1, 2. Pereinama iš 0 į 1, užtat atsiranda papildoma šaknis {$x_1-x_0=x_1$}. D šeima apibrėžia vidinį nulį sutapatinant -1 ir 1, taip kad skaičiavimas vyksta -3, -2, -1=1, 2, 3. Pereinama iš -2 į 1, užtat atsiranda papildoma šaknis {$x_1-(-x_2)=x_1+x_2$}. O C šeima tiesiog suduria abu skaičiavimus: -2, -1, 1, 2. Pereinama iš -1 į 1 užtat atsiranda papildoma šaknis {$x_1-(-x_1)=2x_1$}.
Visa tai turint omenyje, dabar paaiškinsiu, kaip galima suprasti klasikinių Lie algebrų šaknų sistemas. Galime jų paprastasias šaknis {$x_2-x_1$}, {$x_3-x_2$} ir taip toliau suprasti, kaip koduojančius skaičiavimą, 1, 2, 3 ir toliau iki skaičaus n. A šeima skaičiuoja toliau, {$x_{n+1}-x_n$}. Įsidėmėkime, yra dualizmas, kuriuo iš vieno galo skaičiuodami pirmyn 1, 2, 3 tuo pačiu iš kito galo skaičiuojame atgal -3, -2, -1. Kitos trys šeimos skirtingais būdais susieja šias dvi skaičiavimo kryptis. B šeima įveda papildomą, išorinį nulį, tuštumą, {$x_0=0$}, taip kad skaičiavimas vyksta -2, -1, 0, 1, 2. Pereinama iš 0 į 1, užtat atsiranda papildoma šaknis {$x_1-x_0=x_1$}. D šeima apibrėžia vidinį nulį sutapatinant -1 ir 1, taip kad skaičiavimas vyksta -3, -2, -1=1, 2, 3. Pereinama iš -2 į 1, užtat atsiranda papildoma šaknis {$x_1-(-x_2)=x_1+x_2$}. O C šeima tiesiog suduria abu skaičiavimus: -2, -1, 1, 2. Pereinama iš -1 į 1 užtat atsiranda papildoma šaknis {$x_1-(-x_1)=2x_1$}.
Koordinačių sistemos.
Kryžminiai politopai ir kubai. Židinys ir visuma.
Viena politopų šeima yra simpleksai, kuriuos galime generuoti taip. Pradėkime nuo tuščio židinio ir duokime tam židiniui vis pagimdyti po vieną viršūnę.
Viena politopų šeima yra simpleksai, kuriuos galime generuoti taip. Pradėkime nuo tuščio židinio ir duokime tam židiniui vis pagimdyti po vieną viršūnę. Viena viršūnė, tai taškas. Antra
Viena politopų šeima yra simpleksai, kuriuos galime generuoti taip. Pradėkime nuo tuščio židinio ir duokime tam židiniui vis pagimdyti po vieną viršūnę.
Gyvenime nesimetriškos priešingybės pavyzdys yra būti ar nebūti, o simetriškos priešingybės pavyzdys yra būti vienaip ar būti kitaip. Ši plonybė iškyla mąstant kintamųjų sandaugas, jas modeliuojant binomo teorema, Paskalio trikampiu, ir skirtingai interpruojant politopais.
Matematikos priešingybių rūšys: rinktis ar nesirinkti. Rinktis vienaip ar rinktis kitaip. Nesimetriška: 1 ir -1. Simetriška: i ir j.
Gyvenime nesimetriškos priešingybės pavyzdys yra būti ar nebūti, o simetriškos priešingybės pavyzdys yra būti vienokiu ar būti kitokiu. Ši plonybė pasireiškia mąstant kintamųjų sandaugas, jas modeliuojant binomo teorema, Paskalio trikampiu, ir skirtingai interpruojant politopais.
Tuo tarpu skaičiaus {$-1$} dvi šaknys, i ir j, yra iš esmės neatskiriamos. Nėra vidinio pagrindo atskirti posūkį į kairę nuo posūkio į dešinę. Juk {$i \times i = j \times j = -1$}. Tai yra du jungtiniai ir negalime pasakyti, kuri šaknis vadintina i ir kuri vadintina j. Užtat pedagogiškai save labai klaidiname kai tas šaknis vadiname i ir -i, juk kokybiškai jos visiškai nesiskiria, tuo tarpu 1 ir -1 skiriasi.
Tuo tarpu skaičiaus {$-1$} dvi šaknys, i ir j, yra iš esmės neatskiriamos. Nėra vidinio pagrindo atskirti posūkį į kairę nuo posūkio į dešinę. Juk {$i \times i = j \times j = -1$}. Tai yra du jungtiniai ir negalime pasakyti, kuri šaknis vadintina i ir kuri vadintina j. Užtat pedagogiškai save labai klaidiname kai tas šaknis vadiname i ir -i, tarsi viena būtų pagrindinė o kita šalutinė, juk kokybiškai jos visiškai nesiskiria, tuo tarpu 1 ir -1 skiriasi.
Gyvenime
Gyvenime nesimetriškos priešingybės pavyzdys yra būti ar nebūti, o simetriškos priešingybės pavyzdys yra būti vienaip ar būti kitaip. Ši plonybė iškyla mąstant kintamųjų sandaugas, jas modeliuojant binomo teorema, Paskalio trikampiu, ir skirtingai interpruojant politopais.
Tuo tarpu skaičiaus {$-1$} dvi šaknys, i ir j, yra iš esmės neatskiriamos. Nėra vidinio pagrindo atskirti posūkį į kairę nuo posūkio į dešinę. Juk {$i \times $i = $j \times $j = -1$}. Tai yra du jungtiniai ir negalime pasakyti, kuri šaknis vadintina i ir kuri vadintina j. Užtat pedagogiškai save labai klaidiname kai tas šaknis vadiname i ir -i, juk kokybiškai jos visiškai nesiskiria, tuo tarpu 1 ir -1 skiriasi.
Tuo tarpu skaičiaus {$-1$} dvi šaknys, i ir j, yra iš esmės neatskiriamos. Nėra vidinio pagrindo atskirti posūkį į kairę nuo posūkio į dešinę. Juk {$i \times i = j \times j = -1$}. Tai yra du jungtiniai ir negalime pasakyti, kuri šaknis vadintina i ir kuri vadintina j. Užtat pedagogiškai save labai klaidiname kai tas šaknis vadiname i ir -i, juk kokybiškai jos visiškai nesiskiria, tuo tarpu 1 ir -1 skiriasi.
Tuo tarpu skaičiaus {$-1$} dvi šaknys, i ir j, yra iš esmės neatskiriamos. Nėra vidinio pagrindo atskirti posūkį į kairę nuo posūkio į dešinę. Juk {$i \times $i = $j \times $j = -1$}. Tai yra du jungtiniai ir negalime pasakyti, kuri šaknis vadintina i ir kuri vadintina j. Užtat pedagogiškai save labai klaidiname kai tas šaknis vadiname i ir -i, juk kokybiškai jos visiškai nesiskiria, tuo tarpu 1 ir -1 skiriasi.
Gyvenime
Pirmiausia atkreipiu dėmesį, kad matematikoje susiduriame su dviem skirtingomis priešingybių rūšimis, simetriškomis priešingybėmis ir nesimetriškomis priešingybėmis. Nesimetriškos priešingybės pavyzdys yra kada renkamės dauginti iš 1 arba -1. Mes galime atskirti šias dvi galimybes, nes {$1 \times 1 = 1$}, tuo tarpu {$-1 \times -1 \neq -1$} bet {$-1 \times –1 = 1$}. Užtat yra pagrindas vieną priešingybę nepažymėti, o kitą priešingybę pažymėti, kaip jos neigimą.
Pirmiausia atkreipiu dėmesį, kad matematikoje susiduriame su dviem skirtingomis priešingybių rūšimis, simetriškomis priešingybėmis ir nesimetriškomis priešingybėmis. Nesimetriškos priešingybės pavyzdys yra kada renkamės dauginti iš 1 arba -1. Mes galime atskirti šias dvi galimybes, nes {$1 \times 1 = 1$}, tuo tarpu {$-1 \times -1 \neq -1$} bet {$-1 \times -1 = 1$}. Užtat yra pagrindas vieną priešingybę nepažymėti, o kitą priešingybę pažymėti, kaip jos neigimą.
Pirmiausia atkreipiu dėmesį, kad matematikoje susiduriame su dviem skirtingomis priešingybių rūšimis, simetriškomis priešingybėmis ir nesimetriškomis priešingybėmis. Pavyzdžiui, kai renkamės dauginti iš 1 arba -1, mes galime atskirti šias dvi galimybes, nes {$1 \times 1 = 1$}, tuo tarpu {$-1 \times -1 \neq -1$} bet {$-1 \times –1 = 1$}
Pirmiausia atkreipiu dėmesį, kad matematikoje susiduriame su dviem skirtingomis priešingybių rūšimis, simetriškomis priešingybėmis ir nesimetriškomis priešingybėmis. Nesimetriškos priešingybės pavyzdys yra kada renkamės dauginti iš 1 arba -1. Mes galime atskirti šias dvi galimybes, nes {$1 \times 1 = 1$}, tuo tarpu {$-1 \times -1 \neq -1$} bet {$-1 \times –1 = 1$}. Užtat yra pagrindas vieną priešingybę nepažymėti, o kitą priešingybę pažymėti, kaip jos neigimą.
- rinktis ar nesirinkti
- rinktis vienaip ar kitaip ar nesirinkti
- rinktis ar nesirinkti vienaip ar nesirinkti kitaip
- rinktis vienaip ar rinktis kitaip = nesirinkti vienaip ar nesirinkti kitaip
- išsirinkti ar neišsirinkti
- išsirinkti vienaip ar išsirinkti kitaip ar neišsirinkti
- išsirinkti ar neišsirinkti vienaip ar neišsirinkti kitaip
- išsirinkti vienaip ar išsirinkti kitaip = neišsirinkti vienaip ar neišsirinkti kitaip
Atvirkštinės matricos koduoja santykius tarp indeksus.
Pirmiausia atkreipiu dėmesį, kad matematikoje susiduriame su dviem skirtingomis priešingybių rūšimis, simetriškomis priešingybėmis ir nesimetriškomis priešingybėmis. Pavyzdžiui, kai renkamės dauginti iš 1 arba -1, mes galime atskirti šias dvi galimybes, nes {$1 \times 1 = 1$}, tuo tarpu {$-1 \times –1 \neq 1$} bet {$-1 \times –1 = 1$}
Pirmiausia atkreipiu dėmesį, kad matematikoje susiduriame su dviem skirtingomis priešingybių rūšimis, simetriškomis priešingybėmis ir nesimetriškomis priešingybėmis. Pavyzdžiui, kai renkamės dauginti iš 1 arba -1, mes galime atskirti šias dvi galimybes, nes {$1 \times 1 = 1$}, tuo tarpu {$-1 \times -1 \neq -1$} bet {$-1 \times –1 = 1$}
Pirmiausia atkreipiu dėmesį, kad matematikoje susiduriame su dviem skirtingomis priešingybių rūšimis, simetriškomis priešingybėmis ir nesimetriškomis priešingybėmis. Pavyzdžiui, kai renkamės dauginti iš 1 arba -1, mes galime atskirti šias dvi galimybes, nes {$1 \times 1 = 1$}, tuo tarpu {$-1 \times –1 = 1$}
Pirmiausia atkreipiu dėmesį, kad matematikoje susiduriame su dviem skirtingomis priešingybių rūšimis, simetriškomis priešingybėmis ir nesimetriškomis priešingybėmis. Pavyzdžiui, kai renkamės dauginti iš 1 arba -1, mes galime atskirti šias dvi galimybes, nes {$1 \times 1 = 1$}, tuo tarpu {$-1 \times –1 \neq 1$} bet {$-1 \times –1 = 1$}
Pirmiausia atkreipiu dėmesį, kad matematikoje susiduriame su dviem skirtingomis priešingybių rūšimis, simetriškomis priešingybėmis ir nesimetriškomis priešingybėmis. Pavyzdžiui, kai renkamės dauginti iš 1 arba -1, mes galime atskirti šias dvi galimybes, nes {$1 \times 1 = 1$}, tuo tarpu {$-1 \times –1 = 1$}
- rinktis/nesirinkti vienaip ar rinktis/nesirinkti kitaip
- rinktis vienaip ar rinktis kitaip = nesirinkti vienaip ar nesirinkti kitaip
Yra tokios grynos galimybės iš kurių toliau gali būti suduriamos mišrio galimybės.
Yra tokios grynos galimybės iš kurių toliau gali būti suduriamos mišrios galimybės.
Skaičiavimas: 1, 2, 3, ... yra tuo pačiu -3, -2, -1. Galima susieti abu skaičiavimus.
Politopai.
Palyginkime klasikinių Lie algebrų šaknų sistemas. Galime jų paprastasias šaknis {$x_2-x_1$}, {$x_3-x_2$} ir taip toliau suprasti, kaip koduojančius skaičiavimą, 1, 2, 3 ir toliau iki skaičaus n. A šeima skaičiuoja toliau, {$x_{n+1}-x_n$}. Iš tikrųjų, yra dualizmas, kuriuo iš vieno galo skaičiuodami pirmyn 1, 2, 3 tuo pačiu iš kito galo skaičiuojame atgal -3, -2, -1. Kitos trys šeimos skirtingais būdais susieja šias dvi skaičiavimo kryptis. B šeima įveda papildomą, išorinį nulį, tuštumą, {$x_0=0$}, taip kad skaičiavimas vyksta -2, -1, 0, 1, 2. Pereinama iš 0 į 1, užtat atsiranda papildoma šaknis {$x_1-x_0=x_1$}. D šeima apibrėžia vidinį nulį sutapatinant -1 ir 1, taip kad skaičiavimas vyksta -3, -2, -1=1, 2, 3. Pereinama iš -2 į 1, užtat atsiranda papildoma šaknis {$x_1-(-x_2)=x_1+x_2$}. O C šeima tiesiog suduria abu skaičiavimus: -2, -1, 1, 2. Pereinama iš -1 į 1 užtat atsiranda papildoma šaknis {$x_1-(-x_1)=2x_1$}.
Tai jau žingsnis pirmyn link paaiškinimo kurio ieškau. Manau, jis taip pat gali padėti suprasti realiųjų skaičių, kompleksinių skaičių ir kvaternionų vaidmenį. Mat A šeima susijusi su unitarinėmis matricomis, su kompleksinių skaičių norma, su posūkiais kompleksinių skaičių daugiamatėje erdvėje, tad skaičiavimo dualizmas gali glūdėti kompleksinių skaičių jungtiniuose. B ir D šeimos susijusios su neporinių ir porinių dimensijų ortogonalinėmis matricomis, su realųjų skaičių norma, su posūkiais realųjų skaičių daugiamatėje erdvėje. Jas galima suprasti kaip skaičiavimo sukarpymą ir galus sudūrimą. Tuos galus galima sudurti papildomu matu, ir tokiu atveju bus neporinis matų skaičius. Arba galima du matus sutapatinti, kuriuo atveju yra porinis matų skaičius. O C šeima susijusi su simplektinėmis matricomis, su kvaternionų norma, su posūkiais kvartenionų daugiamatėje erdvėje. Ją galima suprasti kaip skaičiavimo sulankstymą, taip kad iš dviejų matų gaunasi keturi matai.
Palyginkime klasikinių Lie algebrų šaknų sistemas. Galime jų paprastasias šaknis {$x_2-x_1$}, {$x_3-x_2$} ir taip toliau suprasti, kaip koduojančius skaičiavimą, 1, 2, 3 ir toliau iki skaičaus n. A šeima skaičiuoja toliau, {$x_{n+1}-x_n$}. Iš tikrųjų, yra dualizmas, kuriuo iš vieno galo skaičiuodami pirmyn 1, 2, 3 tuo pačiu iš kito galo skaičiuojame atgal -3, -2, -1. Kitos trys šeimos skirtingais būdais susieja šias dvi skaičiavimo kryptis. B šeima įveda papildomą, išorinį nulį, tuštumą, {$x_0=0$}, taip kad skaičiavimas vyksta -2, -1, 0, 1, 2. Pereinama iš 0 į 1, užtat atsiranda papildoma šaknis {$x_1-x_0=x_1$}. D šeima apibrėžia vidinį nulį sutapatinant -1 ir 1, taip kad skaičiavimas vyksta -3, -2, -1=1, 2, 3. Pereinama iš -2 į 1, užtat atsiranda papildoma šaknis {$x_1-(-x_2)=x_1+x_2$}. O C šeima tiesiog suduria abu skaičiavimus: -2, -1, 1, 2. Pereinama iš -1 į 1 užtat atsiranda papildoma šaknis {$x_1-(-x_1)=2x_1$}.
Tai jau žingsnis pirmyn link paaiškinimo kurio ieškau. Manau, jis taip pat gali padėti suprasti realiųjų skaičių, kompleksinių skaičių ir kvaternionų vaidmenį. Mat A šeima susijusi su unitarinėmis matricomis, su kompleksinių skaičių norma, su posūkiais kompleksinių skaičių daugiamatėje erdvėje, tad skaičiavimo dualizmas gali glūdėti kompleksinių skaičių jungtiniuose. B ir D šeimos susijusios su neporinių ir porinių dimensijų ortogonalinėmis matricomis, su realųjų skaičių norma, su posūkiais realųjų skaičių daugiamatėje erdvėje. Jas galima suprasti kaip skaičiavimo sukarpymą ir galus sudūrimą. Tuos galus galima sudurti papildomu matu, ir tokiu atveju bus neporinis matų skaičius. Arba galima du matus sutapatinti, kuriuo atveju yra porinis matų skaičius. O C šeima susijusi su simplektinėmis matricomis, su kvaternionų norma, su posūkiais kvartenionų daugiamatėje erdvėje. Ją galima suprasti kaip skaičiavimo sulankstymą, taip kad iš dviejų matų gaunasi keturi matai.
Matematikos priešingybių rūšys: rinktis ar nesirinkti. Rinktis vienaip ar rinktis kitaip. 1 ir -1. i ir j.
Keturios galimybės:
Matematikos priešingybių rūšys: rinktis ar nesirinkti. Rinktis vienaip ar rinktis kitaip. Nesimetriška: 1 ir -1. Simetriška: i ir j.
Keturios galimybės, kaip protui nusiteikti:
Yra tokios grynos galimybės iš kurių toliau gali būti suduriamos mišrio galimybės.
Jos išsako simetrijas slypiančias pačioje matematikoje, tai yra, bet kurioje sandaugoje, bet kurioje pasirinkimų grandinėje. Pristatysiu keturis skirtingus būdus, kaip galime mąstyti pasirinkimų grandinę.
Išmąsčiau, kad keturios klasikinės šeimos išsako simetrijas slypiančias pačioje matematikoje, tai yra, bet kurioje sandaugoje, bet kurioje pasirinkimų grandinėje. Pristatysiu keturis skirtingus būdus, kaip galime mąstyti pasirinkimų grandinę.
- rinktis vienaip ar rinktis kitaip = nesirinkti vienaip ar nesirinkti kitaip
- rinktis/nesirinkti vienaip ar rinktis/nesirinkti kitaip
- rinktis vienaip ar rinktis kitaip
- rinktis vienaip ar rinktis kitaip = nesirinkti vienaip ar nesirinkti kitaip
Keturios galimybės:
- rinktis ar nesirinkti
- rinktis vienaip ar kitaip ar nesirinkti
- rinktis ar nesirinkti vienaip ar nesirinkti kitaip
- rinktis vienaip ar rinktis kitaip
Priešingybės: rinktis ar nesirinkti. Rinktis vienaip ar rinktis kitaip.
Matematikos priešingybių rūšys: rinktis ar nesirinkti. Rinktis vienaip ar rinktis kitaip. 1 ir -1. i ir j.
Jos išsako simetrijas slypiančias sandaugoje, pasirinkimų grandinėje.
Jos išsako simetrijas slypiančias pačioje matematikoje, tai yra, bet kurioje sandaugoje, bet kurioje pasirinkimų grandinėje. Pristatysiu keturis skirtingus būdus, kaip galime mąstyti pasirinkimų grandinę.
Priešingybės: rinktis ar nesirinkti. Rinktis vienaip ar rinktis kitaip.
Lie teorija yra, mano manymu, siaubingai abstrakti, tačiau jos išdavos yra netikėtai dalykiškos. Jų galimybes išsako pavaizduotos Dynkin diagramos. Yra keturios begalinės, klasikinės šeimos ir penkios papildomos išimtys. Mane domina, kaip paprasčiausiai suprasti ir paaiškinti, kuomi pasižymi šios klasikinės šeimos ir kodėl jų yra būtent keturios. Gal man pavyks per trumpą laiką jus įtikinti, kad turėtų slypėti kol kas neatrastas, gilus bet paprastas atsakymas. Pasidalinsiu su jumis kelias savo įžvalgas.
Lie teorija yra, mano manymu, siaubingai abstrakti, tačiau jos išdavos yra netikėtai dalykiškos. Jų galimybes išsako pavaizduotos Dynkin diagramos. Yra keturios begalinės, klasikinės šeimos ir penkios papildomos išimtys. Mane domina, kaip paprasčiausiai suprasti ir paaiškinti, kuomi pasižymi šios klasikinės šeimos ir kodėl jų yra būtent keturios.
Jos išsako simetrijas slypiančias sandaugoje, pasirinkimų grandinėje.
Prieš trejus metus pasiryžau atsekti, kokiais samprotavimais išsivysto visa matematika, jos paskiros šakos, sąvokos, klausimai, atsakymai, tyrimo būdai. Pradžiai pasidariau matematikos šakų klasifikacijos žemėlapį, pamąsčiau kuri šaka kuria remiasi. Bendrais bruožais, matematika plasnoja dviem sparnais, analize ir algebra, kuriuos sieja daugiamatė geometrija. Analizės ir algebros sąsają išsako atitikimas tarp kompaktinių Lie grupių ir paprastųjų Lie algebrų. Iš esmės, kompaktinė Lie grupė yra matricų grupė išreiškianti daugiamačius posūkius, o paprastoji Lie algebra yra tų posūkių ašių simetrijų lentelė. Šios erdvės ir simetrijos riboja įmanomas geometrijas ir sudaro teoretinės fizikos abėcėlę.
Prieš trejus metus pasiryžau atsekti, kokiais samprotavimais išsivysto visa matematika, jos paskiros šakos, sąvokos, klausimai, atsakymai, tyrimo būdai. Pradžiai pasidariau matematikos šakų klasifikacijos žemėlapį, pamąsčiau kuri šaka kuria remiasi. Bendrais bruožais, matematika plasnoja dviem sparnais, analize ir algebra, kuriuos sieja daugiamatė geometrija. Analizės ir algebros sąsają išsako atitikimas tarp kompaktinių Lie grupių ir paprastųjų Lie algebrų. Iš esmės, kompaktinė Lie grupė yra matricų grupė išreiškianti daugiamačius posūkius, o paprastoji Lie algebra yra tų posūkių ašių sankabų simetrijų lentelė. Šios erdvės ir simetrijos riboja įmanomas geometrijas ir sudaro teoretinės fizikos abėcėlę.
Vaikystėje užsimojau viską žinoti ir tą žinojimą gražiai taikyti. Besąlygiška tiesa išsakytina sandaromis, o matematika yra sandarų mokslas. Tad 1993-čiaisiais metais būtent iš matematikos, algebrainės kombinatorikos, gavau daktaro laipsnį iš Kalifornijos universiteto San Diege.
Esu filosofas. Vaikystėje užsimojau viską žinoti ir tą žinojimą gražiai taikyti. Besąlygiška tiesa išsakytina sandaromis, o matematika yra sandarų mokslas. Tad 1993-čiaisiais metais būtent iš matematikos, algebrainės kombinatorikos, gavau daktaro laipsnį iš Kalifornijos universiteto San Diege.
Vaikystėje užsimojau viską žinoti ir tą žinojimą gražiai taikyti. Išmintis išsakoma sandaromis, o matematika yra sandarų mokslas. Tad 1993-čiaisiais metais būtent iš matematikos, algebrainės kombinatorikos, gavau daktaro laipsnį iš Kalifornijos universiteto San Diege.
Vaikystėje užsimojau viską žinoti ir tą žinojimą gražiai taikyti. Besąlygiška tiesa išsakytina sandaromis, o matematika yra sandarų mokslas. Tad 1993-čiaisiais metais būtent iš matematikos, algebrainės kombinatorikos, gavau daktaro laipsnį iš Kalifornijos universiteto San Diege.
- I) Matematikos žemėlapis ir Lie algebros, Lie grupės
I) Matematikos žemėlapis ir Lie algebros, Lie grupės
- II) Sandaugos simetrijos - politopai - priešingybės
- III) Nulis
II) Sandaugos simetrijos
- politopai - priešingybės
III) Nulis
- IV) Atvirkštinės matricos
IV) Atvirkštinės matricos
Palyginkime klasikinių Lie algebrų šaknų sistemas. Galime jų paprastasias šaknis {$x_2-x_1$}, {$x_3-x_2$} ir taip toliau suprasti, kaip koduojančius skaičiavimą, 1, 2, 3 ir toliau iki skaičaus n. A šeima skaičiuoja toliau, {$x_{n+1}-x_n$}. Iš tikrųjų, yra dualizmas, kuriuo iš vieno galo skaičiuodami pirmyn 1, 2, 3 tuo pačiu iš kito galo skaičiuojame atgal -3, -2, -1. Kitos trys šeimos skirtingais būdais susieja šias dvi skaičiavimo kryptis. B šeima įveda papildomą, išorinį nulį, tuštumą, {$x_0=0$}, taip kad skaičiavimas vyksta -2, -1, 0, 1, 2. Pereinama iš 0 į 1, užtat atsiranda papildoma šaknis {$x_1-x_0=x_1-0=x_1$}. D šeima apibrėžia vidinį nulį sutapatinant -1 ir 1, taip kad skaičiavimas vyksta -3, -2, -1=1, 2, 3. Pereinama iš -2 į 1, užtat atsiranda papildoma šaknis {$x_1-(-x_2)=x_1+x_2$}. O C šeima tiesiog suduria abu skaičiavimus: -2, -1, 1, 2. Pereinama iš -1 į 1 užtat atsiranda papildoma šaknis {$x_1-(-x_1)=2x_1$}.
Palyginkime klasikinių Lie algebrų šaknų sistemas. Galime jų paprastasias šaknis {$x_2-x_1$}, {$x_3-x_2$} ir taip toliau suprasti, kaip koduojančius skaičiavimą, 1, 2, 3 ir toliau iki skaičaus n. A šeima skaičiuoja toliau, {$x_{n+1}-x_n$}. Iš tikrųjų, yra dualizmas, kuriuo iš vieno galo skaičiuodami pirmyn 1, 2, 3 tuo pačiu iš kito galo skaičiuojame atgal -3, -2, -1. Kitos trys šeimos skirtingais būdais susieja šias dvi skaičiavimo kryptis. B šeima įveda papildomą, išorinį nulį, tuštumą, {$x_0=0$}, taip kad skaičiavimas vyksta -2, -1, 0, 1, 2. Pereinama iš 0 į 1, užtat atsiranda papildoma šaknis {$x_1-x_0=x_1$}. D šeima apibrėžia vidinį nulį sutapatinant -1 ir 1, taip kad skaičiavimas vyksta -3, -2, -1=1, 2, 3. Pereinama iš -2 į 1, užtat atsiranda papildoma šaknis {$x_1-(-x_2)=x_1+x_2$}. O C šeima tiesiog suduria abu skaičiavimus: -2, -1, 1, 2. Pereinama iš -1 į 1 užtat atsiranda papildoma šaknis {$x_1-(-x_1)=2x_1$}.
Palyginkime klasikinių Lie algebrų šaknų sistemas. Galime jų paprastasias šaknis {$x_2-x_1$}, {$x_3-x_2$} ir taip toliau suprasti, kaip koduojančius skaičiavimą, 1, 2, 3 ir toliau iki skaičaus n. A šeima skaičiuoja toliau, {$x_{n+1}-x_n$}. Iš tikrųjų, yra dualizmas, kuriuo iš vieno galo skaičiuodami pirmyn 1, 2, 3 tuo pačiu iš kito galo skaičiuojame atgal -3, -2, -1. Kitos trys šeimos skirtingais būdais susieja šias dvi skaičiavimo kryptis. B šeima įveda papildomą, išorinį nulį, tuštumą, taip kad skaičiavimas vyksta -2, -1, 0, 1, 2. Pereinama iš 0 į 1, užtat atsiranda papildoma šaknis {$x_1-0=x_1$}. D šeima apibrėžia vidinį nulį sutapatinant -1 ir 1, taip kad skaičiavimas vyksta -3, -2, -1=1, 2, 3. Pereinama iš -2 į 1, užtat atsiranda papildoma šaknis {$x_1-(-x_2)=x_1+x_2$}. O C šeima tiesiog suduria abu skaičiavimus: -2, -1, 1, 2. Pereinama iš -1 į 1 užtat atsiranda papildoma šaknis {$x_1-(-x_1)=2x_1$}.
Palyginkime klasikinių Lie algebrų šaknų sistemas. Galime jų paprastasias šaknis {$x_2-x_1$}, {$x_3-x_2$} ir taip toliau suprasti, kaip koduojančius skaičiavimą, 1, 2, 3 ir toliau iki skaičaus n. A šeima skaičiuoja toliau, {$x_{n+1}-x_n$}. Iš tikrųjų, yra dualizmas, kuriuo iš vieno galo skaičiuodami pirmyn 1, 2, 3 tuo pačiu iš kito galo skaičiuojame atgal -3, -2, -1. Kitos trys šeimos skirtingais būdais susieja šias dvi skaičiavimo kryptis. B šeima įveda papildomą, išorinį nulį, tuštumą, {$x_0=0$}, taip kad skaičiavimas vyksta -2, -1, 0, 1, 2. Pereinama iš 0 į 1, užtat atsiranda papildoma šaknis {$x_1-x_0=x_1-0=x_1$}. D šeima apibrėžia vidinį nulį sutapatinant -1 ir 1, taip kad skaičiavimas vyksta -3, -2, -1=1, 2, 3. Pereinama iš -2 į 1, užtat atsiranda papildoma šaknis {$x_1-(-x_2)=x_1+x_2$}. O C šeima tiesiog suduria abu skaičiavimus: -2, -1, 1, 2. Pereinama iš -1 į 1 užtat atsiranda papildoma šaknis {$x_1-(-x_1)=2x_1$}.
- IV) Kaip susikabina posūkiai
- Komutatyvumas - apskritimas - nulis
- Posūkių grupės - aspkritimas, sfera
- IV) Atvirkštinės matricos
- Skaičiai - realusis: posūkis taške - joks, kompleksinis: posūkis apskritime, kvaternionas: posūkis sferoje
- V) Skaičiai - realusis: posūkis taške - joks, kompleksinis: posūkis apskritime, kvaternionas: posūkis sferoje (?)
- Inverse elements
- Kaip susikabina posūkiai
- Komutatyvumas - apskritimas - nulis
- Posūkių grupės - aspkritimas, sfera
Žr. Classical Lie Algebras, Santrauka
Žr. Classical Lie Algebras, Santrauka, Juodraštis
Palyginkime klasikinių Lie algebrų šaknų sistemas. Galime jų paprastasias šaknis {$x_2-x_1$}, {$x_3-x_2$} ir taip toliau suprasti, kaip koduojančius skaičiavimą, 1, 2, 3 ir toliau iki skaičaus n. A šeima skaičiuoja toliau, {$x_n+1-x_n$}. Iš tikrųjų, yra dualizmas, kuriuo iš vieno galo skaičiuodami pirmyn 1, 2, 3 tuo pačiu iš kito galo skaičiuojame atgal -3, -2, -1. Kitos trys šeimos skirtingais būdais susieja šias dvi skaičiavimo kryptis. B šeima įveda papildomą, išorinį nulį, taip kad skaičiavimas vyksta -2, -1, 0, 1, 2. Pereinama iš 0 į 1, užtat atsiranda papildoma šaknis {$x_1-0=x_1$}. D šeima apibrėžia vidinį nulį sutapatinant -1 ir 1, taip kad skaičiavimas vyksta -3, -2, -1=1, 2, 3. Pereinama iš -2 į 1, užtat atsiranda papildoma šaknis {$x_1-(-x_2)=x_1+x_2$}. O C šeima tiesiog suduria abu skaičiavimus: -2, -1, 1, 2. Pereinama iš -1 į 1 užtat atsiranda papildoma šaknis {$x_1-(-x_1)=2x_1$}.
Palyginkime klasikinių Lie algebrų šaknų sistemas. Galime jų paprastasias šaknis {$x_2-x_1$}, {$x_3-x_2$} ir taip toliau suprasti, kaip koduojančius skaičiavimą, 1, 2, 3 ir toliau iki skaičaus n. A šeima skaičiuoja toliau, {$x_{n+1}-x_n$}. Iš tikrųjų, yra dualizmas, kuriuo iš vieno galo skaičiuodami pirmyn 1, 2, 3 tuo pačiu iš kito galo skaičiuojame atgal -3, -2, -1. Kitos trys šeimos skirtingais būdais susieja šias dvi skaičiavimo kryptis. B šeima įveda papildomą, išorinį nulį, tuštumą, taip kad skaičiavimas vyksta -2, -1, 0, 1, 2. Pereinama iš 0 į 1, užtat atsiranda papildoma šaknis {$x_1-0=x_1$}. D šeima apibrėžia vidinį nulį sutapatinant -1 ir 1, taip kad skaičiavimas vyksta -3, -2, -1=1, 2, 3. Pereinama iš -2 į 1, užtat atsiranda papildoma šaknis {$x_1-(-x_2)=x_1+x_2$}. O C šeima tiesiog suduria abu skaičiavimus: -2, -1, 1, 2. Pereinama iš -1 į 1 užtat atsiranda papildoma šaknis {$x_1-(-x_1)=2x_1$}.
Tai jau žingsnis pirmyn link paaiškinimo kurio ieškau. Manau, jis taip pat gali padėti suprasti realiųjų skaičių, kompleksinių skaičių ir kvaternionų vaidmenį. Mat A šeima susijusi su unitarinėmis matricomis, su kompleksinių skaičių norma, su posūkiais kompleksinių skaičių daugiamatėje erdvėje, tad skaičiavimo dualizmas gali glūdėti kompleksinių skaičių jungtiniuose. B ir D šeimos susijusios su neporinių ir porinių dimensijų ortogonalinėmis matricomis, su realųjų skaičių norma, su posūkiais realųjų skaičių daugiamatėje erdvėje. Jas galima suprasti kaip skaičiavimo sukarpymą ir galus sudūrimą. Tuos galus galima sudurti papildomu matu, ir tokiu atveju bus neporinis matų skaičius. Arba galima du matus sutapatinti, kuriuo atveju yra porinis matų skaičius. O C šeima susijusi su simplektinėmis matricomis, su kvaternionų norma, su posūkiais kvartenionų daugiamatėje erdvėje. Ją galima suprasti kaip skaičiavimo sulankstymą, taip kad iš dviejų matų gaunasi keturi matai.
Palyginkime klasikinių Lie algebrų šaknų sistemas. Galime jų paprastasias šaknis {$x_2-x_1$}, {$x_3-x_2$} ir taip toliau suprasti, kaip koduojančius skaičiavimą, 1, 2, 3 ir toliau.
Palyginkime klasikinių Lie algebrų šaknų sistemas. Galime jų paprastasias šaknis {$x_2-x_1$}, {$x_3-x_2$} ir taip toliau suprasti, kaip koduojančius skaičiavimą, 1, 2, 3 ir toliau iki skaičaus n. A šeima skaičiuoja toliau, {$x_n+1-x_n$}. Iš tikrųjų, yra dualizmas, kuriuo iš vieno galo skaičiuodami pirmyn 1, 2, 3 tuo pačiu iš kito galo skaičiuojame atgal -3, -2, -1. Kitos trys šeimos skirtingais būdais susieja šias dvi skaičiavimo kryptis. B šeima įveda papildomą, išorinį nulį, taip kad skaičiavimas vyksta -2, -1, 0, 1, 2. Pereinama iš 0 į 1, užtat atsiranda papildoma šaknis {$x_1-0=x_1$}. D šeima apibrėžia vidinį nulį sutapatinant -1 ir 1, taip kad skaičiavimas vyksta -3, -2, -1=1, 2, 3. Pereinama iš -2 į 1, užtat atsiranda papildoma šaknis {$x_1-(-x_2)=x_1+x_2$}. O C šeima tiesiog suduria abu skaičiavimus: -2, -1, 1, 2. Pereinama iš -1 į 1 užtat atsiranda papildoma šaknis {$x_1-(-x_1)=2x_1$}.
Klasikinių Lie algebrų šaknų sistemų augimą galima suprasti taip. Paprasčiausia yra
Palyginkime klasikinių Lie algebrų šaknų sistemas. Galime jų paprastasias šaknis {$x_2-x_1$}, {$x_3-x_2$} ir taip toliau suprasti, kaip koduojančius skaičiavimą, 1, 2, 3 ir toliau.
Klasikinių Lie algebrų šaknų sistemų augimą galima suprasti taip. Paprasčiausia yra
Šaknų sistemos yra navigacinės sistemos. Svarbu, kad neatsirastų dvi šaknys rodančios ta pačia kryptimi. Tokiu atveju visa sistema subliukštų, tai yra, atitinkama Cartano matrica išsigimtų, neturėtų atvirkštinės, jos determinantas būtų nulis. Galima įsitikinti, kad šaknų sistema negali susidaryti iš kubo šonų ir kampų, mat, tuomet kubo šono kryptimi atsirastų dvigubai ilgesnė šaknis.
Šaknų sistemos yra navigacinės sistemos. Svarbu, kad neatsirastų dvi šaknys rodančios ta pačia kryptimi. Tokiu atveju visa sistema subliukštų, tai yra, atitinkama Cartano matrica išsigimtų, neturėtų atvirkštinės, jos determinantas būtų nulis. Galima įsitikinti, kad šaknų sistema negali susidaryti iš kubo šonų ir kampų, mat, tuomet kubo šono kryptimi atsirastų dvigubai ilgesnė šaknis. O tai reiškia, kad sistema negali neribotai augti trimis kryptimis ir iš esmės tegali augti, kaip grandinė.
Aišku, nelengva įsivaizduoti šias daugiamates sistemas, tačiau kai kurios galūnės yra dvimatės sistemos. Šie keli pavyzdžiai pavaizduoja šaknų sistemų simetriškumą. Kiekviena šaknis α nusako savitą kryptį, ir kaip normali vektorė apibrėžia hiperplokštumą. Visų šaknų atspindžiai kitapus tos hiperplokštumos taipogi bus šaknys, įskaitant ir −α. Užtat jeigu dvi šaknis skiria daugiau kaip 90 laipsnių kampas, tai jų sudėtis bus šaknis. Ir jeigu dvi šaknis skiria mažiau kaip 90 laipsnių kampas, tai jų skirtumas bus šaknis. Bet jeigu šaknis skiria lygiai 90 laipsnių kampas, tai jų sudėtis ar skirtumas gali būti ar nebūti šaknų sistemoje, žiūrint kokia sistema. Šiaip kai šaknis skiria 120 laipsnių kampas, kaip kad šaknų grandinėje, tai visos šaknys yra tokio pat ilgio. Tačiau galūnėje paskutinę šaknį gali skirti 135 laipsnių kampas, kuomet jinai bus už visas kitas trumpesnė arba už visas kitas ilgesnė.
Aišku, nelengva įsivaizduoti šias daugiamates sistemas, tačiau kai kurios galūnės yra dvimatės sistemos. Šie keli pavyzdžiai pavaizduoja šaknų sistemų simetriškumą. Kiekviena šaknis α nusako savitą kryptį, ir kaip normali vektorė apibrėžia hiperplokštumą. Visų šaknų atspindžiai kitapus tos hiperplokštumos taipogi bus šaknys, įskaitant ir −α. Užtat jeigu dvi šaknis skiria daugiau kaip 90 laipsnių kampas, tai jų sudėtis bus šaknis. Ir jeigu dvi šaknis skiria mažiau kaip 90 laipsnių kampas, tai jų skirtumas bus šaknis. Bet jeigu šaknis skiria lygiai 90 laipsnių kampas, tai jų sudėtis ar skirtumas gali būti ar nebūti šaknų sistemoje, žiūrint kokia sistema. Šiaip kai šaknis skiria 120 laipsnių kampas, kaip kad šaknų grandinėje, tai visos šaknys yra tokio pat ilgio. Tačiau galūnėje paskutinę šaknį gali skirti 135 laipsnių kampas, kuomet jinai bus už visas kitas trumpesnė arba už visas kitas ilgesnė.
Šaknų sistemos yra navigacinės sistemos. Svarbu, kad neatsirastų dvi šaknys rodančios ta pačia kryptimi. Tokiu atveju visa sistema subliukštų, tai yra, atitinkama Cartano matrica išsigimtų, neturėtų atvirkštinės, jos determinantas būtų nulis. Galima įsitikinti, kad šaknų sistema negali susidaryti iš kubo šonų ir kampų, mat, tuomet kubo šono kryptimi atsirastų dvigubai ilgesnė šaknis.
Dynkin diagrama vaizduoja Lie algebros paprastasias šaknis, tai yra, vienamates erdves, kurių prireikia nusakant Lie grupės posūkius. Kiekvienas rutulėlis yra vienamatė erdvė, šaknis, vektorius. Dynkin diagrama koduoja ryšius tarp šaknų. Geometriškai, dvigubas ryšys tarp šaknų reiškia jas skiria 135 laipsnių kampas, viengubas ryšys tarp šaknų reiškia jas skiria 120 laipsnių kampas, o jeigu nėra ryšio tarp šaknų, tai jas skiria 90 laipsnių kampas, vadinasi, jos yra ortogonalios, nesąveikauja. Žodžiu, šaknų sąveikavimas labai ribotas, jos vienas kitai beveik visada ortogonalios. Įsidėmėkime, kad visos keturios klasikinės šeimos yra labai panašios, skiriasi tiktai galūnės. Kiekvienu atveju stuburą daro šaknų grandinė. 120 laipsnių kampu pereiname iš pirmos šaknies į antrą šaknį, ir 120 laipsnių kampu pereiname iš antros šaknies į trečią šaknį, tačiau pirmą ir trečią šaknį skiria būtent 90 laipsnių, taip kad jos tiesiogiai nesąveikauja. Ir taip per visą grandinę ir kitokių grandinių negali būti. Tad labai įdomu, kas darosi tose galūnėse.
Prisipažįstu, aš kol kas tik pradinukas bandydamas įsivaizduoti posūkius ir kaip juos vaizduoti matricomis, kurių nariai gali būti realieji skaičiai, kompleksiniai skaičiai arba netgi kvaternionai. Paprasčiausi yra posūkiai apskritime, kuriuos galima vaizduoti realiųjų skaičių matricomis dviem eilutėm ir dviem stulpeliais, arba vienu kompleksiniu skaičiumi. Šie posūkiai yra komutatyvūs, užtat neįdomūs, tarsi nuliniai. Tačiau šį apskritimą, kurio posūkiai sukasi apie {$z$} ašį, galime papildyti posūkiais apie {$x$} ir {$y$} ašis. Šiuos posūkius apie sferą galima pavaizduoti vienu kvaternionu. Dabar jau atsiranda nekomutatyvumas. Posūkis apie {$x$} ir paskui {$y$} skiriasi nuo posūkio apie {$y$} ir paskui {$x$}. Atsiranda tarsi sankaba tarp šių dviejų galimybių ir jų ryšį išreiškia komutatorius XY-YX = [X,Y]. Kai šis komutatorius nulinis, tai posūkiai nesusiję, bet kai jis nenulinis, tai posūkiai sąveikauja, o būtent tai mus domina. Turbūt ne tik man yra sunku įsivaizduoti posūkius keturmatėse ir penkiamatėse erdvėse, nes Lie grupių klausimai nagrinėjami Lie algebromis, kurie susieti eksponencialu, taip kad posūkių daugybos klausimai virsta sankabų sudėties klausimais.
Dynkin diagrama vaizduoja Lie algebros paprastasias šaknis, tai yra, vienamates erdves, kurių prireikia nusakant Lie grupės posūkius. Kiekvienas rutulėlis yra vienamatė erdvė, šaknis, vektorius, tarsi ta sankaba siejanti sferos posūkius. Dynkin diagrama koduoja ryšius tarp šaknų, tarp tų sankabų. Geometriškai, dvigubas ryšys tarp šaknų reiškia jas skiria 135 laipsnių kampas, viengubas ryšys tarp šaknų reiškia jas skiria 120 laipsnių kampas, o jeigu nėra ryšio tarp šaknų, tai jas skiria 90 laipsnių kampas, vadinasi, jos yra ortogonalios, nesąveikauja. Žodžiu, šaknų sąveikavimas labai ribotas, jos vienas kitai beveik visada ortogonalios. Įsidėmėkime, kad visos keturios klasikinės šeimos yra labai panašios, skiriasi tiktai galūnės. Kiekvienu atveju stuburą daro šaknų grandinė. 120 laipsnių kampu pereiname iš pirmos šaknies į antrą šaknį, ir 120 laipsnių kampu pereiname iš antros šaknies į trečią šaknį, tačiau pirmą ir trečią šaknį skiria būtent 90 laipsnių, taip kad jos tiesiogiai nesąveikauja. Ir taip per visą grandinę ir kitokių grandinių negali būti. Tad labai įdomu, kas darosi tose galūnėse.
Aišku, nelengva įsivaizduoti šias daugiamates sistemas, tačiau kai kurios galūnės yra dvimatės sistemos. Šie keli pavyzdžiai pavaizduoja šaknų sistemų simetriškumą. Kiekviena šaknis {$\alpha$} kaip normali vektorė apibrėžia hiperplokštumą, ir visų šaknų atspindžiai kitapus tos hiperplokštumos taipogi bus šaknys, įskaitant ir {$-\alpha$}. Užtat jeigu dvi šaknis skiria daugiau kaip 90 laipsnių kampas, tai jų sudėtis bus šaknis. Ir jeigu dvi šaknis skiria mažiau kaip 90 laipsnių kampas, tai jų skirtumas bus šaknis. Bet jeigu šaknis skiria lygiai 90 laipsnių kampas, tai jų sudėtis ar skirtumas gali būti ar nebūti šaknų sistemoje, žiūrint kokia sistema.
Aišku, nelengva įsivaizduoti šias daugiamates sistemas, tačiau kai kurios galūnės yra dvimatės sistemos. Šie keli pavyzdžiai pavaizduoja šaknų sistemų simetriškumą. Kiekviena šaknis α nusako savitą kryptį, ir kaip normali vektorė apibrėžia hiperplokštumą. Visų šaknų atspindžiai kitapus tos hiperplokštumos taipogi bus šaknys, įskaitant ir −α. Užtat jeigu dvi šaknis skiria daugiau kaip 90 laipsnių kampas, tai jų sudėtis bus šaknis. Ir jeigu dvi šaknis skiria mažiau kaip 90 laipsnių kampas, tai jų skirtumas bus šaknis. Bet jeigu šaknis skiria lygiai 90 laipsnių kampas, tai jų sudėtis ar skirtumas gali būti ar nebūti šaknų sistemoje, žiūrint kokia sistema. Šiaip kai šaknis skiria 120 laipsnių kampas, kaip kad šaknų grandinėje, tai visos šaknys yra tokio pat ilgio. Tačiau galūnėje paskutinę šaknį gali skirti 135 laipsnių kampas, kuomet jinai bus už visas kitas trumpesnė arba už visas kitas ilgesnė.
Aišku, nelengva įsivaizduoti šias daugiamates sistemas, tačiau kai kurios galūnės yra dvimatės sistemos. Šie keli pavyzdžiai pavaizduoja šaknų sistemų simetriškumą. Kiekviena šaknis {$\alpha$} kaip normali vektorė apibrėžia hiperplokštumą, ir visų šaknų atspindžiai kitapus tos hiperplokštumos taipogi bus šaknys, įskaitant ir {$-\alpha$}.
Aišku, nelengva įsivaizduoti šias daugiamates sistemas, tačiau kai kurios galūnės yra dvimatės sistemos. Šie keli pavyzdžiai pavaizduoja šaknų sistemų simetriškumą. Kiekviena šaknis {$\alpha$} kaip normali vektorė apibrėžia hiperplokštumą, ir visų šaknų atspindžiai kitapus tos hiperplokštumos taipogi bus šaknys, įskaitant ir {$-\alpha$}. Užtat jeigu dvi šaknis skiria daugiau kaip 90 laipsnių kampas, tai jų sudėtis bus šaknis. Ir jeigu dvi šaknis skiria mažiau kaip 90 laipsnių kampas, tai jų skirtumas bus šaknis. Bet jeigu šaknis skiria lygiai 90 laipsnių kampas, tai jų sudėtis ar skirtumas gali būti ar nebūti šaknų sistemoje, žiūrint kokia sistema.
Aišku, nelengva įsivaizduoti šias daugiamates sistemas, tačiau kai kurios galūnės yra dvimatės sistemos, visai gražios ir mums artimos savo simetrija.
Aišku, nelengva įsivaizduoti šias daugiamates sistemas, tačiau kai kurios galūnės yra dvimatės sistemos. Šie keli pavyzdžiai pavaizduoja šaknų sistemų simetriškumą. Kiekviena šaknis {$\alpha$} kaip normali vektorė apibrėžia hiperplokštumą, ir visų šaknų atspindžiai kitapus tos hiperplokštumos taipogi bus šaknys, įskaitant ir {$-\alpha$}.
Dynkin diagrama vaizduoja Lie algebros paprastasias šaknis, tai yra, vienamates erdves, kurių prireikia nusakant Lie grupės posūkius. Kiekvienas rutulėlis yra vienamatė erdvė, šaknis, vektorius. Dynkin diagrama koduoja ryšius tarp šaknų. Geometriškai, dvigubas ryšys tarp šaknų reiškia jas skiria 135 laipsnių kampas, viengubas ryšys tarp šaknų reiškia jas skiria 120 laipsnių kampas, o jeigu nėra ryšio tarp šaknų, tai jas skiria 90 laipsnių kampas, vadinasi, jos yra ortogonalios, nesąveikauja. Žodžiu, šaknų saveikavimas labai ribotas, jos vienas kitai beveik visada ortogonalios. Įsidėmėkime, kad visos keturios klasikinės šeimos yra labai panašios, skiriasi tiktai galūnės. Kiekvienu atveju stuburą daro šaknų grandinė. 120 laipsnių kampu pereiname iš pirmos šaknies į antrą šaknį, ir 120 laipsnių kampu pereiname iš antros šaknies į trečią šaknį, tačiau pirmą ir trečią šaknį skiria būtent 90 laipsnių, taip kad jos tiesiogiai nesąveikauja. Ir taip per visą grandinę ir kitokių grandinių negali būti. Tad labai įdomu, kas darosi tose galūnėse.
Dynkin diagrama vaizduoja Lie algebros paprastasias šaknis, tai yra, vienamates erdves, kurių prireikia nusakant Lie grupės posūkius. Kiekvienas rutulėlis yra vienamatė erdvė, šaknis, vektorius. Dynkin diagrama koduoja ryšius tarp šaknų. Geometriškai, dvigubas ryšys tarp šaknų reiškia jas skiria 135 laipsnių kampas, viengubas ryšys tarp šaknų reiškia jas skiria 120 laipsnių kampas, o jeigu nėra ryšio tarp šaknų, tai jas skiria 90 laipsnių kampas, vadinasi, jos yra ortogonalios, nesąveikauja. Žodžiu, šaknų sąveikavimas labai ribotas, jos vienas kitai beveik visada ortogonalios. Įsidėmėkime, kad visos keturios klasikinės šeimos yra labai panašios, skiriasi tiktai galūnės. Kiekvienu atveju stuburą daro šaknų grandinė. 120 laipsnių kampu pereiname iš pirmos šaknies į antrą šaknį, ir 120 laipsnių kampu pereiname iš antros šaknies į trečią šaknį, tačiau pirmą ir trečią šaknį skiria būtent 90 laipsnių, taip kad jos tiesiogiai nesąveikauja. Ir taip per visą grandinę ir kitokių grandinių negali būti. Tad labai įdomu, kas darosi tose galūnėse.
Dynkin diagrama vaizduoja Lie algebros paprastasias šaknis, tai yra, vienamates erdves, kurių prireikia nusakant Lie grupės posūkius. Kiekvienas rutulėlis yra vienamatė erdvė, šaknis, vektorius. Dynkin diagrama koduoja ryšius tarp šaknų. Geometriškai, dvigubas ryšys tarp šaknų reiškia juos skiria 135 laipsnių kampas, viengubas ryšys tarp šaknų reiškia juos skiria 120 laipsnių kampas, o jeigu nėra ryšio tarp šaknų, tai juos skiria 90 laipsnių kampas, vadinasi, jie yra ortogonalūs, nesąveikauja. Įsidėmėkime, kad visos keturios klasikinės šeimos yra labai panašios, skiriasi tiktai galūnės. Kiekvienu atveju stuburą daro šaknų grandinė. 120 laipsnių kampu pereiname iš pirmos šaknies į antrą šaknį, ir 120 laipsnių kampu pereiname iš antros šaknies į trečią šaknį, tačiau pirmą ir trečią šaknį skiria būtent 90 laipsnių, taip kad jos tiesiogiai nesąveikauja. Ir taip per visą grandinę ir kitokių grandinių negali būti. Tad labai įdomu, kad darosi tose galūnėse.
Dynkin diagrama vaizduoja Lie algebros paprastasias šaknis, tai yra, vienamates erdves, kurių prireikia nusakant Lie grupės posūkius. Kiekvienas rutulėlis yra vienamatė erdvė, šaknis, vektorius. Dynkin diagrama koduoja ryšius tarp šaknų. Geometriškai, dvigubas ryšys tarp šaknų reiškia jas skiria 135 laipsnių kampas, viengubas ryšys tarp šaknų reiškia jas skiria 120 laipsnių kampas, o jeigu nėra ryšio tarp šaknų, tai jas skiria 90 laipsnių kampas, vadinasi, jos yra ortogonalios, nesąveikauja. Žodžiu, šaknų saveikavimas labai ribotas, jos vienas kitai beveik visada ortogonalios. Įsidėmėkime, kad visos keturios klasikinės šeimos yra labai panašios, skiriasi tiktai galūnės. Kiekvienu atveju stuburą daro šaknų grandinė. 120 laipsnių kampu pereiname iš pirmos šaknies į antrą šaknį, ir 120 laipsnių kampu pereiname iš antros šaknies į trečią šaknį, tačiau pirmą ir trečią šaknį skiria būtent 90 laipsnių, taip kad jos tiesiogiai nesąveikauja. Ir taip per visą grandinę ir kitokių grandinių negali būti. Tad labai įdomu, kas darosi tose galūnėse.
Aišku, nelengva įsivaizduoti šias daugiamates sistemas, tačiau kai kurios galūnės yra dvimatės sistemos, visai gražios ir mums artimos savo simetrija.
Dynkin diagrama vaizduoja Lie algebros paprastasias šaknis, tai yra, vienamates erdves, kurių prireikia nusakant Lie grupės posūkius. Kiekvienas rutulėlis yra vienamatė erdvė, šaknis, vektorius. Dynkin diagrama koduoja ryšius tarp šaknų. Geometriškai, dvigubas ryšys tarp šaknų reiškia juos skiria 135 laipsnių kampas, viengubas ryšys tarp šaknų reiškia juos skiria 120 laipsnių kampas, o jeigu nėra ryšio tarp šaknų, tai juos skiria 90 laipsnių kampas, vadinasi, jie yra ortogonalūs, nesąveikauja. Įsidėmėkime, kad visos keturios klasikinės šeimos yra labai panašios.
Dynkin diagrama vaizduoja Lie algebros paprastasias šaknis, tai yra, vienamates erdves, kurių prireikia nusakant Lie grupės posūkius. Kiekvienas rutulėlis yra vienamatė erdvė, šaknis, vektorius. Dynkin diagrama koduoja ryšius tarp šaknų. Geometriškai, dvigubas ryšys tarp šaknų reiškia juos skiria 135 laipsnių kampas, viengubas ryšys tarp šaknų reiškia juos skiria 120 laipsnių kampas, o jeigu nėra ryšio tarp šaknų, tai juos skiria 90 laipsnių kampas, vadinasi, jie yra ortogonalūs, nesąveikauja. Įsidėmėkime, kad visos keturios klasikinės šeimos yra labai panašios, skiriasi tiktai galūnės. Kiekvienu atveju stuburą daro šaknų grandinė. 120 laipsnių kampu pereiname iš pirmos šaknies į antrą šaknį, ir 120 laipsnių kampu pereiname iš antros šaknies į trečią šaknį, tačiau pirmą ir trečią šaknį skiria būtent 90 laipsnių, taip kad jos tiesiogiai nesąveikauja. Ir taip per visą grandinę ir kitokių grandinių negali būti. Tad labai įdomu, kad darosi tose galūnėse.
Dynkin diagrama vaizduoja se, kiekvienas rutulėlis yra vienamatė erdvė, šaknis, tai yra, Iš Dynkin diagramų matyti, kad keturios klasikinės šeimos yra labai panašios.
Dynkin diagrama vaizduoja Lie algebros paprastasias šaknis, tai yra, vienamates erdves, kurių prireikia nusakant Lie grupės posūkius. Kiekvienas rutulėlis yra vienamatė erdvė, šaknis, vektorius. Dynkin diagrama koduoja ryšius tarp šaknų. Geometriškai, dvigubas ryšys tarp šaknų reiškia juos skiria 135 laipsnių kampas, viengubas ryšys tarp šaknų reiškia juos skiria 120 laipsnių kampas, o jeigu nėra ryšio tarp šaknų, tai juos skiria 90 laipsnių kampas, vadinasi, jie yra ortogonalūs, nesąveikauja. Įsidėmėkime, kad visos keturios klasikinės šeimos yra labai panašios.
Dynkin diagramose, kiekvienas rutulėlis yra vienamatė erdvė, šaknis, tai yra, Iš Dynkin diagramų matyti, kad keturios klasikinės šeimos yra labai panašios.
Dynkin diagrama vaizduoja se, kiekvienas rutulėlis yra vienamatė erdvė, šaknis, tai yra, Iš Dynkin diagramų matyti, kad keturios klasikinės šeimos yra labai panašios.
Lie teorija yra, mano manymu, siaubingai abstrakti, tačiau jos išdavos yra netikėtai dalykiškos. Jų galimybes išsako pavaizduotos Dynkin diagramos. Yra keturios begalinės, klasikinės šeimos ir penkios papildomos išimtys. Mane domina, kaip paprasčiausiai suprasti ir paaiškinti, kuomi pasižymi šios klasikinės šeimos ir kodėl jų yra būtent keturios. Per trumpą laiką aš pasidalinsiu su jumis eilę savo įžvalgų, kurios jums padėtų jei kada pasiryžtumėte labiau įsigilinti.
Lie teorija yra, mano manymu, siaubingai abstrakti, tačiau jos išdavos yra netikėtai dalykiškos. Jų galimybes išsako pavaizduotos Dynkin diagramos. Yra keturios begalinės, klasikinės šeimos ir penkios papildomos išimtys. Mane domina, kaip paprasčiausiai suprasti ir paaiškinti, kuomi pasižymi šios klasikinės šeimos ir kodėl jų yra būtent keturios. Gal man pavyks per trumpą laiką jus įtikinti, kad turėtų slypėti kol kas neatrastas, gilus bet paprastas atsakymas. Pasidalinsiu su jumis kelias savo įžvalgas.
Prieš trejus metus pasiryžau atsekti, kokiais samprotavimais išsivysto visa matematika, jos paskiros šakos, sąvokos, klausimai, atsakymai, tyrimo būdai. Pradžiai pasidariau matematikos šakų klasifikacijos žemėlapį, pamąsčiau kuri šaka kuria remiasi. Bendrais bruožais, matematika plasnoja dviem sparnais, analize ir algebra, kuriuos sieja daugiamatė geometrija. Analizės ir algebros sąsają išsako atitikimas tarp kompaktinių Lie grupių ir paprastųjų Lie algebrų. Iš esmės, kompaktinė Lie grupė yra matricų grupė išreiškianti daugiamačius posūkius, o paprastoji Lie algebra yra tų posūkių ašių simetrijų lentelė. Užtat
Jų klasifikacija Jų teorija yra, mano manymu, siaubingai abstrakti, tačiau jų išdavos yra netikėtai
Prieš trejus metus pasiryžau atsekti, kokiais samprotavimais išsivysto visa matematika, jos paskiros šakos, sąvokos, klausimai, atsakymai, tyrimo būdai. Pradžiai pasidariau matematikos šakų klasifikacijos žemėlapį, pamąsčiau kuri šaka kuria remiasi. Bendrais bruožais, matematika plasnoja dviem sparnais, analize ir algebra, kuriuos sieja daugiamatė geometrija. Analizės ir algebros sąsają išsako atitikimas tarp kompaktinių Lie grupių ir paprastųjų Lie algebrų. Iš esmės, kompaktinė Lie grupė yra matricų grupė išreiškianti daugiamačius posūkius, o paprastoji Lie algebra yra tų posūkių ašių simetrijų lentelė. Šios erdvės ir simetrijos riboja įmanomas geometrijas ir sudaro teoretinės fizikos abėcėlę.
Lie teorija yra, mano manymu, siaubingai abstrakti, tačiau jos išdavos yra netikėtai dalykiškos. Jų galimybes išsako pavaizduotos Dynkin diagramos. Yra keturios begalinės, klasikinės šeimos ir penkios papildomos išimtys. Mane domina, kaip paprasčiausiai suprasti ir paaiškinti, kuomi pasižymi šios klasikinės šeimos ir kodėl jų yra būtent keturios. Per trumpą laiką aš pasidalinsiu su jumis eilę savo įžvalgų, kurios jums padėtų jei kada pasiryžtumėte labiau įsigilinti.
Dynkin diagramose, kiekvienas rutulėlis yra vienamatė erdvė, šaknis, tai yra, Iš Dynkin diagramų matyti, kad keturios klasikinės šeimos yra labai panašios.
Išvysčiau savitą filosofiją. Prieš trejus metus pasiryžau atsekti, kokiais samprotavimais išsivysto visa matematika, jos paskiros šakos, sąvokos, klausimai, atsakymai, tyrimo būdai. Pradžiai pasidariau matematikos šakų klasifikacijos žemėlapį, pamąsčiau kuri šaka kuria remiasi. Bendrais bruožais, matematika plasnoja dviem sparnais, algebra ir analize, kuriuos sieja daugiamatė geometrija. Analizės ir algebros sąsają įspūdingai išreiškia atitikimas tarp Lie grupių ir Lie algebrų ir jų klasifikaciją.
Prieš trejus metus pasiryžau atsekti, kokiais samprotavimais išsivysto visa matematika, jos paskiros šakos, sąvokos, klausimai, atsakymai, tyrimo būdai. Pradžiai pasidariau matematikos šakų klasifikacijos žemėlapį, pamąsčiau kuri šaka kuria remiasi. Bendrais bruožais, matematika plasnoja dviem sparnais, analize ir algebra, kuriuos sieja daugiamatė geometrija. Analizės ir algebros sąsają išsako atitikimas tarp kompaktinių Lie grupių ir paprastųjų Lie algebrų. Iš esmės, kompaktinė Lie grupė yra matricų grupė išreiškianti daugiamačius posūkius, o paprastoji Lie algebra yra tų posūkių ašių simetrijų lentelė. Užtat
Jų klasifikacija Jų teorija yra, mano manymu, siaubingai abstrakti, tačiau jų išdavos yra netikėtai
Išvysčiau savitą filosofiją. Prieš trejus metus pasiryžau atsekti, kokiais samprotavimais išsivysto visa matematika, jos paskiros šakos, sąvokos, klausimai, atsakymai, tyrimo būdai. Pradžiai pasidariau matematikos šakų klasifikacijos žemėlapį, pamąsčiau kuri šaka kuria remiasi. Bendrais bruožais, matematika plasnoja dviem sparnais, algebra ir analize, kuriuos kažkaip sieja žmogišką nuojautą išsakanti geometrija.
Išvysčiau savitą filosofiją. Prieš trejus metus pasiryžau atsekti, kokiais samprotavimais išsivysto visa matematika, jos paskiros šakos, sąvokos, klausimai, atsakymai, tyrimo būdai. Pradžiai pasidariau matematikos šakų klasifikacijos žemėlapį, pamąsčiau kuri šaka kuria remiasi. Bendrais bruožais, matematika plasnoja dviem sparnais, algebra ir analize, kuriuos sieja daugiamatė geometrija. Analizės ir algebros sąsają įspūdingai išreiškia atitikimas tarp Lie grupių ir Lie algebrų ir jų klasifikaciją.
Vaikystėje užsimojau viską žinoti ir tą žinojimą gražiai taikyti. Išmintis išsakoma sandaromis, o matematika yra sandarų mokslas. 1993-čiaisiais metais, Kalifornijos universitete San Diege, gavau daktaro laipsnį iš matematikos, būtent algebrainės kombinatorikos.
Išvysčiau savitą filosofiją. Prieš trejus metus pasiryžau pabandyti atsekti, kokia tvarka protavimu išsivysto visa matematika, jos paskiros šakos, sąvokos, klausimai, atsakymai, tyrimo būdai. Pradžiai pasidariau matematikos šakų klasifikacijos žemėlapį, pamąstyti kuri šaka kuria remiasi. Bendrais bruožais, matematika skrenda dviem sparnais, algebra ir analize, kuriuos kažkaip sieja žmogišką nuojautą išsakanti geometrija.
Vaikystėje užsimojau viską žinoti ir tą žinojimą gražiai taikyti. Išmintis išsakoma sandaromis, o matematika yra sandarų mokslas. Tad 1993-čiaisiais metais būtent iš matematikos, algebrainės kombinatorikos, gavau daktaro laipsnį iš Kalifornijos universiteto San Diege.
Išvysčiau savitą filosofiją. Prieš trejus metus pasiryžau atsekti, kokiais samprotavimais išsivysto visa matematika, jos paskiros šakos, sąvokos, klausimai, atsakymai, tyrimo būdai. Pradžiai pasidariau matematikos šakų klasifikacijos žemėlapį, pamąsčiau kuri šaka kuria remiasi. Bendrais bruožais, matematika plasnoja dviem sparnais, algebra ir analize, kuriuos kažkaip sieja žmogišką nuojautą išsakanti geometrija.
Išvysčiau savitą filosofiją. Prieš trejus metus pasiryžau pabandyti atsekti, kokia tvarka protavimu išsivysto visa matematika, jos paskiros šakos, sąvokos, klausimai, atsakymai, tyrimo būdai. Pradžiai pasidariau matematikos šakų klasifikacijos žemėlapį, pamąstyti kuri šaka kuria remiasi. Bendrais bruožais, matematika skrenda dviem sparnais, algebra ir analize, kuriuos neaišku kaip sieja žmogišką nuojautą išsakanti geometrija.
Išvysčiau savitą filosofiją. Prieš trejus metus pasiryžau pabandyti atsekti, kokia tvarka protavimu išsivysto visa matematika, jos paskiros šakos, sąvokos, klausimai, atsakymai, tyrimo būdai. Pradžiai pasidariau matematikos šakų klasifikacijos žemėlapį, pamąstyti kuri šaka kuria remiasi. Bendrais bruožais, matematika skrenda dviem sparnais, algebra ir analize, kuriuos kažkaip sieja žmogišką nuojautą išsakanti geometrija.
Išvysčiau savitą filosofiją. Prieš trejus metus pasiryžau pabandyti atsekti, kokia tvarka protavimu išsivysto visa matematika, jos paskiros šakos, sąvokos, klausimai, atsakymai, tyrimo būdai. Pradžiai pasidariau matematikos šakų klasifikacijos žemėlapį, pamąstyti kuri šaka kuria remiasi. Bendrais bruožais, matematika skrenda dviem sparnais, algebra ir analize, kuriuos neaišku kaip sieja geometrija.
Išvysčiau savitą filosofiją. Prieš trejus metus pasiryžau pabandyti atsekti, kokia tvarka protavimu išsivysto visa matematika, jos paskiros šakos, sąvokos, klausimai, atsakymai, tyrimo būdai. Pradžiai pasidariau matematikos šakų klasifikacijos žemėlapį, pamąstyti kuri šaka kuria remiasi. Bendrais bruožais, matematika skrenda dviem sparnais, algebra ir analize, kuriuos neaišku kaip sieja žmogišką nuojautą išsakanti geometrija.
Vaikystėje užsimojau viską žinoti ir tą žinojimą gražiai taikyti. Išmintis išsakoma sandaromis, o matematika yra sandarų mokslas. 1993-čiaisiais metais, Kalifornijos universitete San Diege, gavau daktaro laipsnį iš matematikos, būtent algebrainės kombinatorikos.
Išvysčiau savitą filosofiją. Prieš trejus metus pasiryžau pabandyti atsekti, kokia tvarka protavimu išsivysto visa matematika, jos paskiros šakos, sąvokos, klausimai, atsakymai, tyrimo būdai. Pradžiai pasidariau matematikos šakų klasifikacijos žemėlapį, pamąstyti kuri šaka kuria remiasi. Bendrais bruožais, matematika skrenda dviem sparnais, algebra ir analize, kuriuos neaišku kaip sieja geometrija.
- posūkiai turi determinantą 1
- posūkiai turi determinantą 1. So by Cramer's rule they have combinatorially nice inverses.
- Why can't have other inverse type
- Symplectic inverse. How does the symplectic inverse relate to the quaternions? to their conjugation?
- Why can't have other inverse types? For example, i to j iff j-bar to i-bar without sign change?
- Reorganize symplectic matrix in terms of 2x2 matrices. Get combinatorial interpretation of inverse elements.
- Kaip [,] varžo Lie grupes?
- Kaip [,] varžo Lie grupes? If XY=YX, then e^x e^y = e^{x+y} and [X,Y] =0 then dimensions are independent. e^X e^-X = e^I e^(ax+bx) = e^ax e^bx
- Conservation
- Conservation - paths, lines, angles, oriented areas. Sypmlectic 2x2 matrix: oriented area.
- Cartan matrix
- Row of Cartan matrix
- Determinant of Cartan matrix
- Cartan matrix determinant
- Determinant of Cartan matrix of G2 is 1
- Cartan matrix. Entries give the amount of looseness from root -i, how many steps can be taken with root j.
- Row of Cartan matrix. Given root -i, the various degrees of looseness one can take in the direction of each root.
- Determinant of Cartan matrix. Volume of looseness. Shows nondegeneracy of looseness in direction of each root. Volume spanned by row vectors giving looseness from each negative root. Volume spanned by column vectors giving amount of looseness in each direction. Size of WeightLattice/RootLattice which is the looseness of the whole system, the number of times the root system can be repeated in any dimension.
- Cartan matrix determinant. Study why An=n+1. A_n+1=2A_n-A_n-1Why the constraints arise for the other Lie algebra root system. Why the volume collapses for B_n, C_n, D_n. Why it's not possible to alter both ends.
- Determinant of Cartan matrix of G2 is 1. Explain why this is true. Based on Cartan matrix entries, based on weight lattice / root lattice.
- Root systems are variants of A_n simplex. Reverse the count? Why do the quadruple links arise. How does this relate to the Cartan matrix? And the weight lattice? and looseness? For B_n, are these double or quadruple links between x_i and 0?
- Weight/Root = 4 for A_3, show this with a 3-dimensional lattice
- Įvadas į Lie grupes ir algebras.
- Įvadas į Lie grupes ir algebras. Dykin diagrams. Rotations in 2, 3 dimensions. Lie algebra product [,] effect on basis elements of matrices - yeilding ei-ej, aij - arrow
- 120 + 120 = 90 degrees (ir Bott periodicity)
- Link An Lie algebra and Lie group
- An Geometric Link back bone for root systems
- A_2 illustration in 3 dimensions
- požiūriai, matai
- Posūkių grupės - aspkritimas, sfera
- Posūkių grupės - aspkritimas, sfera
- Įvadas į Lie grupes ir algebras.
- Tariamai ar tikrai gyvneimiškai
- Kaip [,] varžo Lie grupes?
- 4 geometrijos
- Conservation
- inverses of group elements
- posūkiai turi determinantą 1
- Inverse types
- Why can't have other inverse type
- posūkiai - R, C, H - ir jų pavyzdžiai mažamatėse erdvėse
- e^tM reikšmės
- poliarinė dekompozicija
- bilinear forms
- matrix symmetries
- Cartan subalgebras
- generalized Cartan matrices
- Cartan matrix
- Row of Cartan matrix
- Determinant of Cartan matrix
- Cartan matrix determinant
- Determinant of Cartan matrix of G2 is 1
- Weight/Root lattice
- Counting <->
- Root systems - simplex enhancements
- Weyl groups
- Choice frameworks
Special linear groups of Reals, Complexes, Quaternions have maximal compact subgroups SO(n), SU(n), Sp(n).
- Posūkių grupės - aspkritimas, sfera, 4-matė
- Posūkių grupės - aspkritimas, sfera
- Posūkių grupės - aspkritimas, sfera
- Posūkių grupės - aspkritimas, sfera, 4-matė
Kaip intuityviai suprasti? Išdėstysiu sąvokas, kurios manau yra svarbios.
- Matematikos žemėlapis ir Lie algebros, Lie grupės
- I) Matematikos žemėlapis ir Lie algebros, Lie grupės
- Sandaugos simetrijos - politopai - priešingybės
- II) Sandaugos simetrijos - politopai - priešingybės
- III) Nulis
- Šaknų sistemos - apsisukimai
- IV) Kaip susikabina posūkiai
- Komutatyvumas - apskritimas - nulis
- Orthogonality of rows and columns - transpose is inverse.
- Ortogonališkumas (eilučių ir stulpelių) Orthogonality of rows and columns - transpose is inverse.
- V) Skaičiai - realusis: posūkis taške - joks, kompleksinis: posūkis apskritime, kvaternionas: posūkis sferoje (?)
- Šaknų sistemos - apsisukimai
- Orthogonality of rows and columns - transpose is inverse.
Andrius Jonas Kulikauskas (Self Learners Network)
Algebra, skaičių teorija ir geometrija
- Matematikos žemėlapis ir Lie algebros, Lie grupės
- Tariamai ar tikrai gyvenimiškai: klasifikavimo išdavos - Dynkin diagramos
- Sandaugos simetrijos - politopai - priešingybės
- Posūkių grupės - aspkritimas, sfera
- Inverse elements
- Šaknų sistemos - apsisukimai
Žr. Classical Lie Algebras
Žr. Classical Lie Algebras, Santrauka
Trečia, klasikinės Lie grupės gerbia skirtingų dalybos algebrų isometrijas. Ortogonalinės, unitarinės, simplektinės grupės atitinkamai gerbia realųjų skaičių, kompleksinių skaičių, kvaternionų isometrijas.
Trečia, klasikines Lie grupes sudaro skirtingų dalybos algebrų isometrijos. Ortogonalinės, unitarinės, simplektinės grupės atitinkamai sudaro realųjų skaičių, kompleksinių skaičių, kvaternionų isometrijos.
Antra, klasikinių Lie algebrų šaknų sistemos skirtingai auga. Visos grupės turi šaknis {$x_1, x_2, \dots , x_n$}. Grupės {$A_n$} šaknys auga toliau {$x_{n+1}$}. Tačiau kitų grupių šaknys įvairiai sieja šį skaičiavimą pirmyn su skaičiavimu atgal {$-x_n, -x_{n-1}, \dots , x_1$}. Grupė {$C_n$} juos suduria tiesiogiai, tarsi sulenkiant siūlą. Taip atsiranda šaknis {$x_n - -x_n = 2x_n$}. Grupė {$B_n$} tarsi karpo skaičiavimo siūlą ir sujungi abi dalis papildomu nuliu {$0$}. Taip atsiranda šaknis {$x_n - 0 = x_n$}. Grupė {$D_n$} tarsi karpo skaičiavimo siūlą ir sutapatina abiejų dalių galus, taip kad {$x_n = -x_n$} ir atsiranda nauja šaknis {$x_n- -x_{n-1} = x_{n-1}+x_n$}. Taigi, klasikinių Lie algebrų šaknų sistemos išsako santykį tarp skaičiavimo pirmyn ir skaičiavimo atgal.
Antra, klasikinių Lie algebrų šaknų sistemos skirtingai auga. Visos grupės turi šaknis {$-x_1+x_2, -x_2 + x_3, \dots , -x_{n-1}+x_{n}$}. Grupės {$A_n$} šaknys auga toliau {$-x_n+x_{n+1}$}. Tačiau kitų grupių šaknys įvairiai sieja šį skaičiavimą pirmyn su skaičiavimu atgal {$-x_n-x_{n-1}, -x_{n-1}-x_{n-2}, \dots , -x_2-x_1$}. Grupė {$C_n$} juos suduria tiesiogiai, tarsi sulenkiant siūlą. Taip atsiranda šaknis {$-x_n -x_n = -2x_n$}. Grupė {$B_n$} tarsi karpo skaičiavimo siūlą ir sujungia abi dalis papildomu nuliu {$0$}. Taip atsiranda šaknis {$-x_n +0 = -x_n$}. Grupė {$D_n$} tarsi karpo skaičiavimo siūlą ir sutapatina abiejų dalių galus, taip kad {$-x_n = -x_n$} ir seka šaknis {$-x_n -x_{n-1}$}. Taigi, klasikinių Lie algebrų šaknų sistemos išsako santykį tarp skaičiavimo pirmyn ir skaičiavimo atgal.
Papasakosime, kaip sekasi tirti ir sieti šiuos tris skirtingus priėjimus, ir kaip jie atkreipia dėmesį į simetrijas glūdinčias pačioje matematikoje, paprasčiausiose jos ženklų išraiškose.
Physical notions of time and space are based on continuity. Mathematically, these notions are modeled by continuous groups, known as Lie groups, and their local behavior at any point is structured and classified by Lie algebras. In particular, there are four infinite families known as the four classical Lie groups and Lie algebras (An, Bn, Cn, Dn). I share my study of the cognitive foundations for why, intuitively, there are these four classical families and what that tells us about time and space.
My particular interest here is to understand how the mind generates and organizes all of mathematics, its various concepts and branches. Lie groups and Lie algebras bring together analysis and algebra, respectively, by way of distinct interfaces, geometries, spatial intuitions.
The classical Lie groups and Lie algebras are infinite families, and so we can explore how they are able to grow to ever higher dimensions. Lie algebras are studied in terms of their highly symmetric root systems, which are "multiplication tables" for adding vectors. I share my philosophical study of how to make sense of the possiblities for these systems, and especially, how they can make sense in ever higher dimensions. I think of the simplest family, An, as propagating a signal ever forward, yielding a sequence:
1-> 2-> .. n-1-> n-> n+1
But I note that the other families reflect the signal backwards in three possible ways:
1-> 2-> .. n-1-> n-> 0-> -n-> -(n-1)-> -(n-2)
1-> 2-> .. n-1-> n-> -n-> -(n-1)-> -(n-2)
1-> 2-> .. n-1-> n-> -(n-1)-> -(n-2)
I am exploring why, cognitively, there are these three types of mirrors for inverting a signal. This all suggests that we should think of time as inherently a duality of forward and backward directions. I argue that this duality is at the heart of the complex numbers, and that the real numbers and quaternions are less fundamental.
I also investigate how intuitive distinctions between the four classical Lie groups/algebras ground the distinction between four geometries: affine, projective, conformal and symplectic. I relate these geometries to the ways that we can think about a triangle as three paths, as three intersecting lines, as three angles, and as the sweeping out of an oriented area.
I conclude with an application to the study of how our emotions help us distinguish the boundary between our selves and our world, for example, between what is sad and what is surprising. I describe six transformations of the boundary - reflection, shear, rotation, dilation, squeeze, translation - as the possible ways of enriching the four geometries, that is, taking us from a less defined geometry to a more defined one. Here again it is possible to look for how spatial geometry (the boundary of one's self) describes the ways of linking time's forward and backward directions (relevant for emotional expectations).
Papasakosime, kaip sekasi tirti ir sieti šiuos tris skirtingus priėjimus, ir kaip jie atkreipia dėmesį į simetrijas glūdinčias pačioje matematikoje, paprasčiausiose jos ženklų išraiškose.
Papasakosime, kaip sekasi tirti ir sieti šiuos tris skirtingus priėjimus, ir kaip jie atkreipia dėmesį į simetrijas glūdinčias pačioje matematikoje, jos paprasčiausiose išraiškose.
Papasakosime, kaip sekasi tirti ir sieti šiuos tris skirtingus priėjimus, ir kaip jie atkreipia dėmesį į simetrijas glūdinčias pačioje matematikoje, paprasčiausiose jos ženklų išraiškose.
Papasakosime, kaip sekasi tirti ir sieti šiuos tris skirtingus priėjimus.
Papasakosime, kaip sekasi tirti ir sieti šiuos tris skirtingus priėjimus, ir kaip jie atkreipia dėmesį į simetrijas glūdinčias pačioje matematikoje, jos paprasčiausiose išraiškose.
Antra, klasikinių Lie algebrų šaknų sistemos skirtingai auga.
Antra, klasikinių Lie algebrų šaknų sistemos skirtingai auga. Visos grupės turi šaknis {$x_1, x_2, \dots , x_n$}. Grupės {$A_n$} šaknys auga toliau {$x_{n+1}$}. Tačiau kitų grupių šaknys įvairiai sieja šį skaičiavimą pirmyn su skaičiavimu atgal {$-x_n, -x_{n-1}, \dots , x_1$}. Grupė {$C_n$} juos suduria tiesiogiai, tarsi sulenkiant siūlą. Taip atsiranda šaknis {$x_n - -x_n = 2x_n$}. Grupė {$B_n$} tarsi karpo skaičiavimo siūlą ir sujungi abi dalis papildomu nuliu {$0$}. Taip atsiranda šaknis {$x_n - 0 = x_n$}. Grupė {$D_n$} tarsi karpo skaičiavimo siūlą ir sutapatina abiejų dalių galus, taip kad {$x_n = -x_n$} ir atsiranda nauja šaknis {$x_n- -x_{n-1} = x_{n-1}+x_n$}. Taigi, klasikinių Lie algebrų šaknų sistemos išsako santykį tarp skaičiavimo pirmyn ir skaičiavimo atgal.
Trečia, klasikinės Lie grupės gerbia skirtingų dalybos algebrų isometrijas. Ortogonalinės, unitarinės, simplektinės grupės atitinkamai gerbia realųjų skaičių, kompleksinių skaičių, kvaternionų isometrijas.
Papasakosime, kaip sekasi tirti ir sieti šiuos tris skirtingus priėjimus.
Keturios klasikinės šeimos Lie grupių ir algebrų yra kertinės matematinės sandaros, siejančios algebrą ir analizę. Jų klasifikacija išplaukia iš Dynkin diagramų. Tai yra unitarinės $A_n$, neporinės ortogonalinės $B_n$, simpleksinės $C_n$ ir porinės ortogonalinės $D_n$ grupės ir algebros. Ar galima giliau ir aiškiau įžvelgti, kokios yra šių keturių šeimų esminės savybės dėl kurių jos išsiskiria?
Keturios klasikinės šeimos Lie grupių ir algebrų yra kertinės matematinės sandaros, siejančios algebrą ir analizę. Jų klasifikacija išplaukia iš Dynkin diagramų. Tai yra unitarinės {$A_n$}, neporinės ortogonalinės {$B_n$}, simplektinės {$C_n$} ir porinės ortogonalinės {$D_n$} grupės ir algebros. Ar galima giliau ir aiškiau įžvelgti, kokios yra šių keturių šeimų esminės savybės dėl kurių jos išsiskiria? Pristatysiu tris priėjimus ir savo pastangas juos susieti.
Pirma, Lie algebrų šaknų sistemas sietinos su jų simetrijas išreiškiančiomis Weyl grupėmis. Atitinkamas simetrijas turi trys politopų šeimos (simpleksai, kryžminiai politopai, hiperkubai) ir ketvirta sandara - hiperkubo koordinačių sistema. Šios keturios sandaros vaizduoja keturių skirtingų pobūdžio pasirinkimų kombinatorikas. Tai skirtingi būdai, kuriais protas įžvelgia simetriją Paskalio trikampiu generuojamoje sandaugoje {$x_1 x_2 \dots x_n$}. Pavyzdžiui, trikampis (simpleksas) turi vieną židinį, tris viršūnes, tris kraštus ir vieną visumą. O pastačius kūbą ant vienos viršūnės, jo aštuonios viršūnės išsidėsto: 1, 3, 3, 1. Atkreipiame dėmesį, kad šios simetrijos paviršutiniškai sutampa tačiau skiriasi savo sintaksine logika.
Antra, klasikinių Lie algebrų šaknų sistemos skirtingai auga.
Keturios klasikinės šeimos Lie grupių ir algebrų yra kertinės matematinės sandaros, siejančios algebrą ir analizę. Jų klasifikacija išplaukia iš Dynkin diagramų. Ar galima giliau ir aiškiau įžvelgti, kokios yra šių keturių šeimų esminės savybęs dėl kurių jos išsiskiria?
Keturios klasikinės šeimos Lie grupių ir algebrų yra kertinės matematinės sandaros, siejančios algebrą ir analizę. Jų klasifikacija išplaukia iš Dynkin diagramų. Tai yra unitarinės $A_n$, neporinės ortogonalinės $B_n$, simpleksinės $C_n$ ir porinės ortogonalinės $D_n$ grupės ir algebros. Ar galima giliau ir aiškiau įžvelgti, kokios yra šių keturių šeimų esminės savybės dėl kurių jos išsiskiria?
Keturios klasikinės šeimos Lie grupių ir algebrų yra kertinės matematinės sandaros, siejančios algebrą ir analizę. Jų klasifikacija išplaukia iš Dynkin diagramų. Ar galima giliau ir aiškiau įžvelgti, kokios yra šių keturių šeimų esminės savybęs dėl kurių jos išsiskiria?
Physical notions of time and space are based on continuity. Mathematically, these notions are modeled by continuous groups, known as Lie groups, and their local behavior at any point is structured and classified by Lie algebras. In particular, there are four infinite families known as the four classical Lie groups and Lie algebras (An, Bn, Cn, Dn). I share my study of the cognitive foundations for why, intuitively, there are these four classical families and what that tells us about time and space.
My particular interest here is to understand how the mind generates and organizes all of mathematics, its various concepts and branches. Lie groups and Lie algebras bring together analysis and algebra, respectively, by way of distinct interfaces, geometries, spatial intuitions.
The classical Lie groups and Lie algebras are infinite families, and so we can explore how they are able to grow to ever higher dimensions. Lie algebras are studied in terms of their highly symmetric root systems, which are "multiplication tables" for adding vectors. I share my philosophical study of how to make sense of the possiblities for these systems, and especially, how they can make sense in ever higher dimensions. I think of the simplest family, An, as propagating a signal ever forward, yielding a sequence:
1-> 2-> .. n-1-> n-> n+1
But I note that the other families reflect the signal backwards in three possible ways:
1-> 2-> .. n-1-> n-> 0-> -n-> -(n-1)-> -(n-2)
1-> 2-> .. n-1-> n-> -n-> -(n-1)-> -(n-2)
1-> 2-> .. n-1-> n-> -(n-1)-> -(n-2)
I am exploring why, cognitively, there are these three types of mirrors for inverting a signal. This all suggests that we should think of time as inherently a duality of forward and backward directions. I argue that this duality is at the heart of the complex numbers, and that the real numbers and quaternions are less fundamental.
I also investigate how intuitive distinctions between the four classical Lie groups/algebras ground the distinction between four geometries: affine, projective, conformal and symplectic. I relate these geometries to the ways that we can think about a triangle as three paths, as three intersecting lines, as three angles, and as the sweeping out of an oriented area.
I conclude with an application to the study of how our emotions help us distinguish the boundary between our selves and our world, for example, between what is sad and what is surprising. I describe six transformations of the boundary - reflection, shear, rotation, dilation, squeeze, translation - as the possible ways of enriching the four geometries, that is, taking us from a less defined geometry to a more defined one. Here again it is possible to look for how spatial geometry (the boundary of one's self) describes the ways of linking time's forward and backward directions (relevant for emotional expectations).
http://www.ms.lt/sodas/Book/20180928ClassicalLieAlgebras
Žr. Classical Lie Algebras
Andrius Jonas Kulikauskas (Self Learners Network)
Keturių klasikinių Lie grupių ir algebrų kombinatorinės ištakos
Algebra, skaičių teorija ir geometrija
http://www.ms.lt/sodas/Book/20180928ClassicalLieAlgebras
LieSandarųIštakos
Naujausi pakeitimai
网站
Įvadas #E9F5FC
Klausimai #FFFFC0
Teiginiai #FFFFFF
Kitų mintys #EFCFE1
Dievas man #FFECC0
Iš ankščiau #CCFFCC
Mieli skaitytojai, visa mano kūryba ir kartu visi šie puslapiai yra visuomenės turtas, kuriuo visi kviečiami laisvai naudotis, dalintis, visaip perkurti. - Andrius
